CKM Constraints from Charmless B Decays
This page features:
|
| Implementation of the Beneke-Buchalla-Neubert-Sachrajda (BBNS) calculations in CkmFitter |
|
| Implementation of the Fleischer-Mannel (FM) and Neubert-Rosner (NR) bounds in CkmFitter |
The calculation of branching ratios and direct CP asymmetries in B->pipi/Kpi decays and the time-dependent asymmetry in B->pi+pi-, within the QCD Factorisation Approach (FA) of BBNS, have been implemented in CkmFitter.
Fits of the BBNS calculation to the branching ratios and direct CP asymmetries of charged and neutral B-decays to pipi and Kpi final states have been performed. Confidence levels are presented in the rhobar-etabar and sin2alpha-sin2beta planes.
The theoretical description of hadronic charmless B-decays is under
ongoing discussion.
Therefore, one should consider these fits as R&D studies
when discussing confidence levels,
e.g. in the rhobar-etabar plane. As a consequence, all plots are
marked by an appropriate R&D logo:
The global fit tests the consistency between data and FA via the best chi-squared found in the fit.
-
We present three different fits here:
- A global fit of BBNS to B->pipi/Kpi branching ratios
- A global fit of BBNS to B->pipi/Kpi branching ratios and direct CP asymmetries ACP
- A global fit of BBNS to B->pipi/Kpi branching ratios in combination with the standard CKM fit
The fit inputs are B-> pipi/Kpi branching ratios measured by BABAR, Belle and CLEO and the CKM element |Vcb| (See the input page and hep-ph/0104062). If not stated otherwise, all branching ratios are understood as CP-averaged branching ratios. We used here the averages taken from BBNS where the experimental errors have been symmetrised:
| BR(B0 -> pi+pi-) | ( 4.4 +/- 0.9)*10^-6 |
| BR(B+ -> pi+pi0) | ( 5.6 +/- 1.5)*10^-6 |
| BR(B0 -> K+ pi-) | (17.2 +/- 1.5)*10^-6 |
| BR(B+ -> K+ pi0) | (12.1 +/- 1.7)*10^-6 |
| BR(B+ -> K0 pi+) | (17.2 +/- 2.5)*10^-6 |
| BR(B0 -> K0 pi0) | (10.3 +/- 2.5)*10^-6 |
| |Vcb| | (40.75 +/- 0.4 +/- 2.0)*10^-3 |
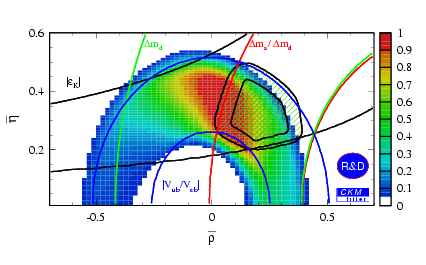
The best fit gives a chi^2 value of 1.82 with 4 degrees of freedom and is found at (rhobar,etabar)=(0.05,3.81). The best fits prefer values for gamma around 90 degrees. The confidence levels obtained show also good agreement with those found in the standard CKM fit:
The constraints obtained in the previous exercise are symmetric under the mapping eta -> -eta. Direct CP asymmetries carry also information on the sign of the CKM angle gamma and hence are sensitive to the sign of eta. In addition to the CP averaged branching ratios used in the previous exercise also direct CP asymmetries of the self-tagging B->Kpi modes are used in this exercise.
We define the direct CP asymmetry ACP as:
|
|
and used averaged results from BABAR, Belle and CLEO:
| ACP(B0->K+-pi-+) | -0.109 +- 0.078 |
| ACP(B0->K+-pi0) | -0.095 +- 0.118 |
| ACP(B0->K0 pi-+) | -0.046 +- 0.136 |
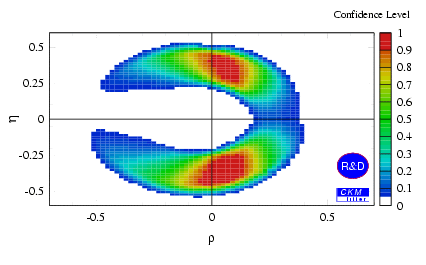
At present, the statistical errors of these measurements are too large to provide a significant test of the FA. The biggest effect of direct CP violation is expected in B0->pi0pi0. However, the fact that the measured direct CP asymmetries are small is consistent with the predictions of the FA. The best fit gives a chi^2 of 2.0 (7 degrees of freedom). Negative values of eta are slightly preferred. This is due to the fact that the BABAR measurement of ACP(B0->K+pi-)=-0.19+/-0.10+/-0.03, though consistent with zero, prefers negative asymmetries, whereas BBNS predicts mainly positive ACP values for positive gamma. It should be noted that the most recent, preliminary BABAR result, ACP(B0->K+pi-)= -0.07+/-0.08+/-0.02, shows even better agreement with BBNS. However, this value was not included in the fit yet.
To test the consistency between the constraints obtained from the BBNS fit to the B->pipi/Kpi branching ratios and those given by the standard CKM fit a combined fit has been performed. Again, a small chi^2 of 2.09 (8 degrees of freedom) is found indicating that FA and the standard CKM fit are consistent at the present stage.
-
The measurement of the time-dependent asymmetry
in B->pi+pi- provides information
on sin(2alpha) if the penguin P over tree T
amplitude ratio is known. Within BBNS the ratio
P/T is calculated. Under the assumption
that the FA is an appropriate description one can
translate the measurement of Spipi into a
constraint in the rhobar-etabar plane.
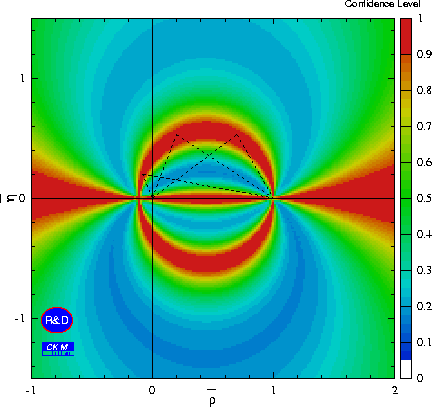
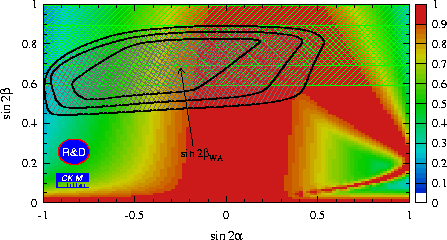
We present here the constraints in the rhobar-etabar and sin2alpha-sin2beta plane from the measurement of Spipi within BBNS. In addition, constraints are shown if the sin2beta world average is used.
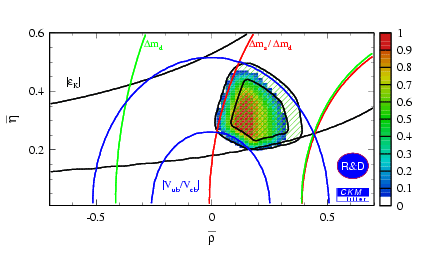
| Constraints in the rhobar-etabar plane from the parameter Spipi, measured by BABAR in a time-dependent B0->pi+pi- analysis, and using the BBNS calculation of the P/T ratio. Theoretical errors as quoted in hep-ph/0104110 (BBNS) have been neglected. Three examples of possible CKM triangles are shown. |
|
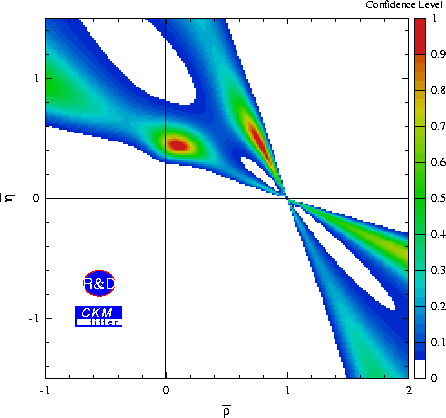
| See figure caption above for more details. The world average of sin2beta has been additionally used in the fit. |
|
| Constraints in the sin2alpha-sin2beta plane from the parameter Spipi. See figure caption above for more details. |
|
Compared to the experimental error of the Spipi measurement from
BABAR,
the theoretical error quoted in the
hep-ph/0104110
(BBNS) is much smaller and was neglected in this exercise.
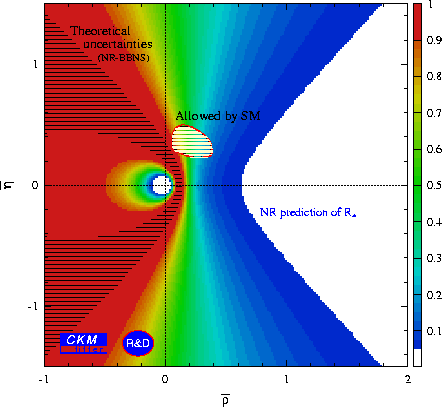
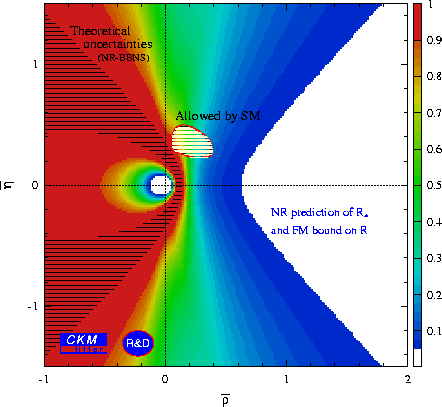
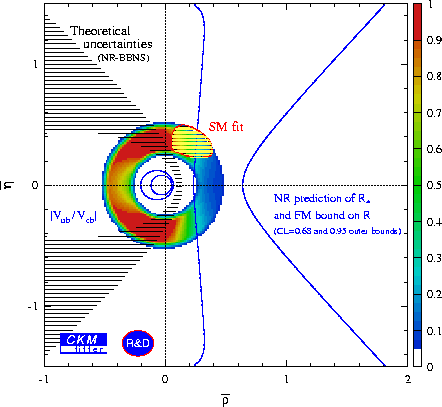
Less prone to theoretical uncertainties but also less predictive are the bounds obtained on the CP-averaged ratios R (FM) and R* (NR), defined by
|
|
|
|
Their respective theoretical predictions have been implemented in CkmFitter. It is assumed for the following plots that the strong phases involved be small, in accordance with the results of the FA. All theoretical parameters used are taken from Ref. hep-ph/0104110.
The tree-to-penguin ratio entering the prediction of R* can be constrained experimentally by means of the ratio
|
|
which introduces correlations due to the common denominator with R*. The same is true when one combines R and R* in a single fit. These correlations are properly introduced in CkmFitter.
-
We shall annotate that the immediate fit input of the ratios
implies the use of asymmetric statistical errors with complicated
probability density functions (see Appendix C in
hep-ph/0104062).
This procedure can be circumvented
by fitting the branching fractions rather than their ratios,
and adjusting simultaneously a free varying scale which is
common to both quantities entering the respective ratios.
We present the results in the rhobar-etabar plane: