CKMfitter

Results as of Lepton-Photon 2005
(preliminary - not yet completed)

Menu:

The Global CKM fit: Inputs and Numerical results

The global CKM fit in the large (ρ-bar,η-bar) plane

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom)

Constraints on the angle α/Φ₂ from charmless B decays

Constraints on the angle γ/Φ₃ from B decays to charm

Constraints on the angle β_s

Constraint from limit on BR(B⁺→τ⁺ ν)

Constraints from b→d penguins

Constraints on |sin(2β+γ)|

Contribution of the different input measurement families to the constraint in the (ρ-bar,η-bar) plane

New physics in B⁰- B⁰-bar Mixing

Numerical results: :

A brief document that provides the collection of up-to-date inputs to the global CKM analysis and the numerical results obtained from it. The results include: Wolfenstein parameters, UT angles, (combinations of) CKM elements, theory parameters and rare branching fractions. Detailed background information on the methodology and the treatment of experimental and theoretical uncertainties is provided in hep-ph/0406184.

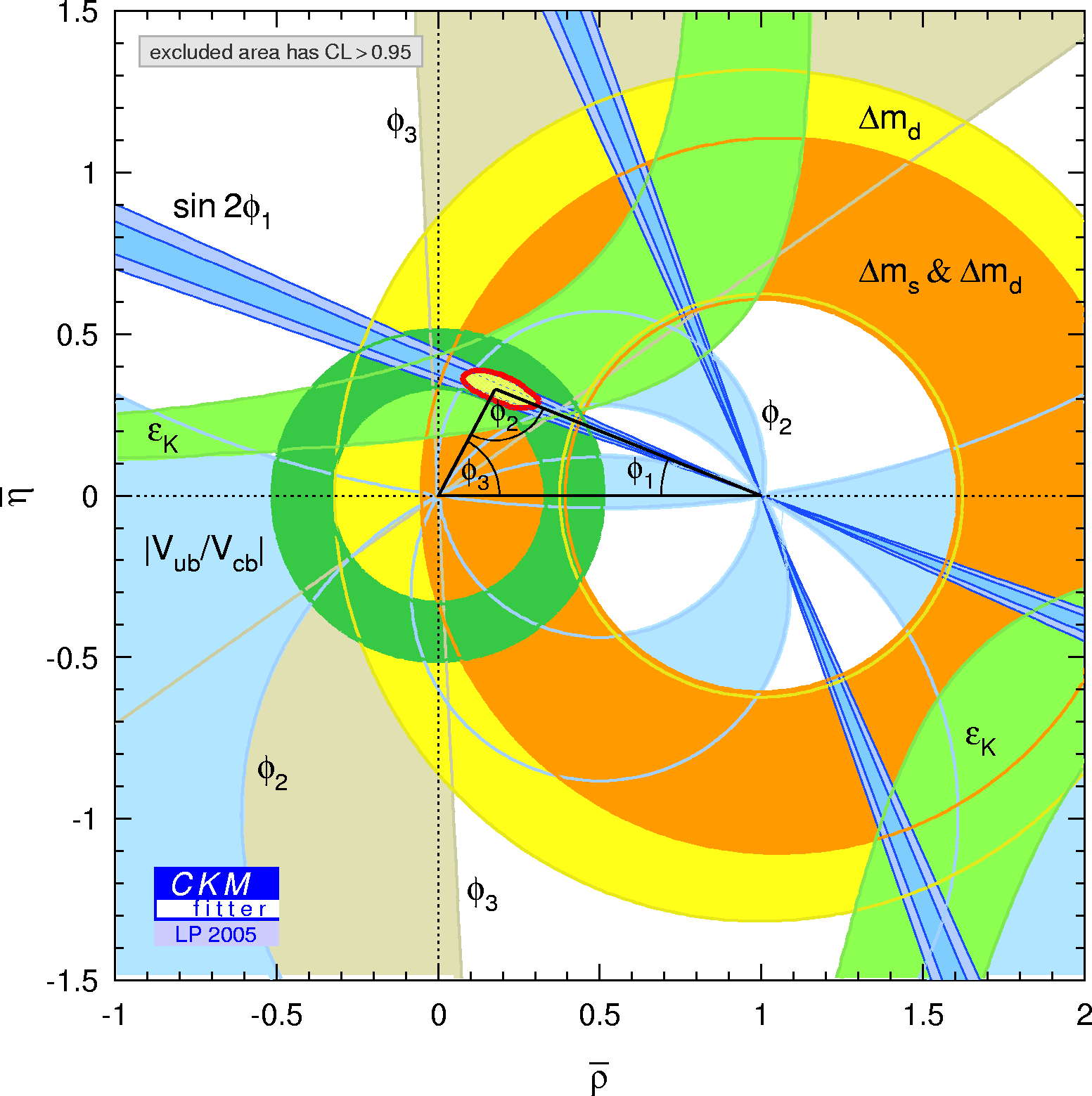
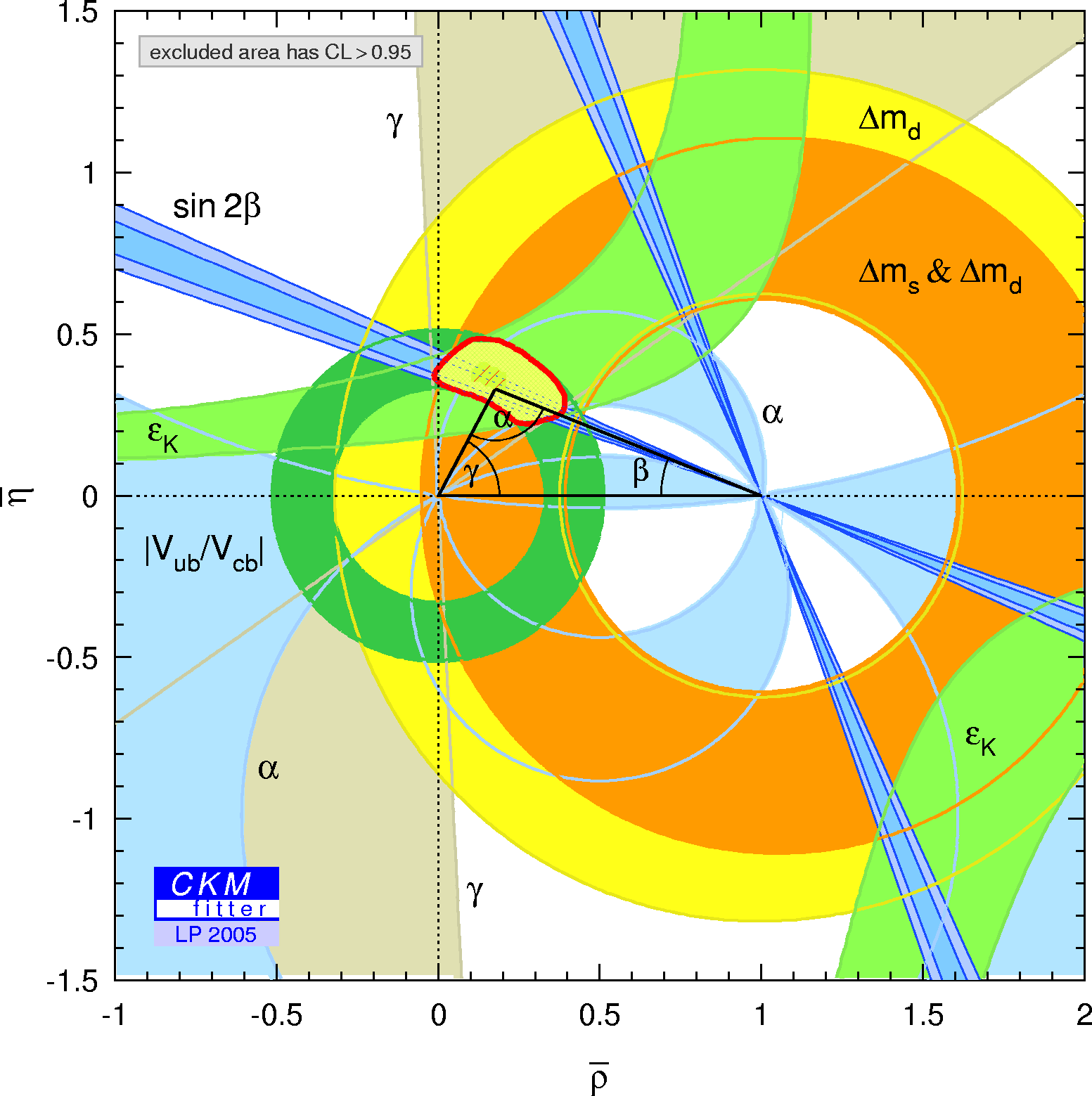
The global CKM fit in the large (ρ-bar,η-bar) plane:

	α,β,γ convention:	φ₁,φ₂,φ₃ convention:
Constraints in the (ρ-bar,η-bar) plane including (a.o.) the most recent α/Φ₂- and γ/Φ₃-related inputs in the global CKM fit.	eps gif	eps gif
Constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit.	eps gif	eps gif
Constraints in the (ρ-bar,η-bar) plane not including the α/Φ₂- and γ/Φ₃ measurements in the global fit.	eps gif	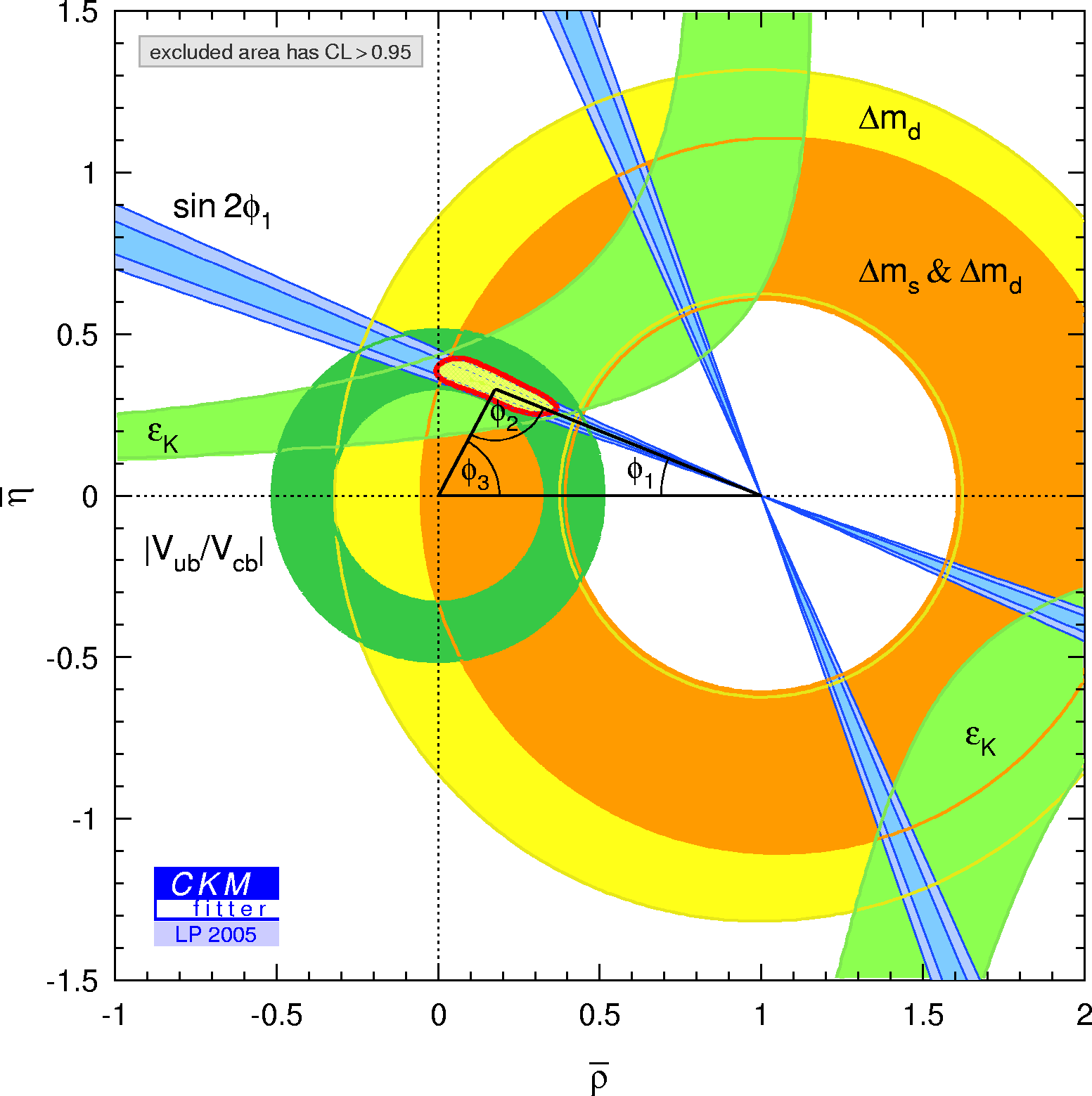eps gif
Constraints in the (ρ-bar,η-bar) plane including only the angle measurements in the global fit.	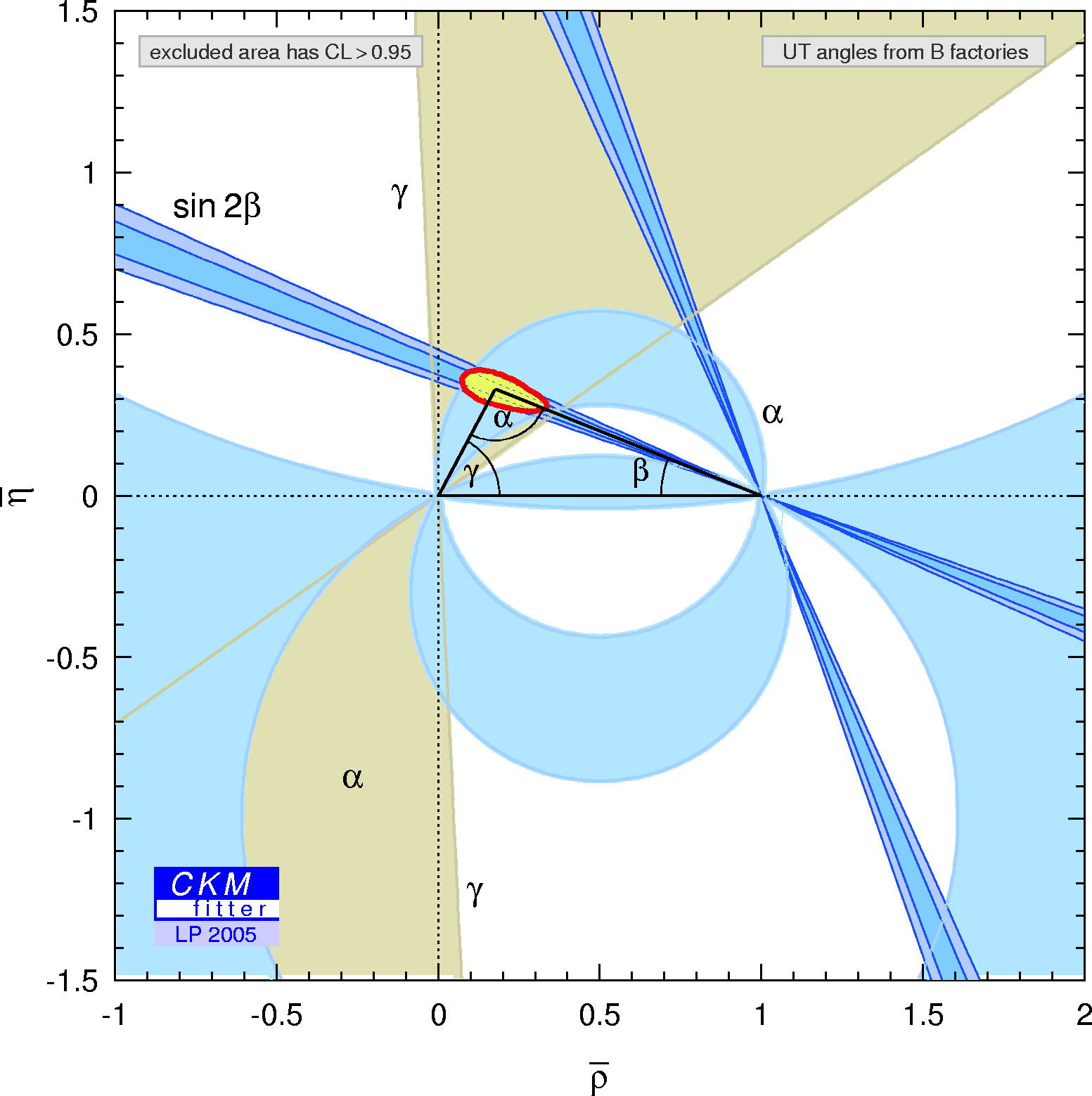eps gif	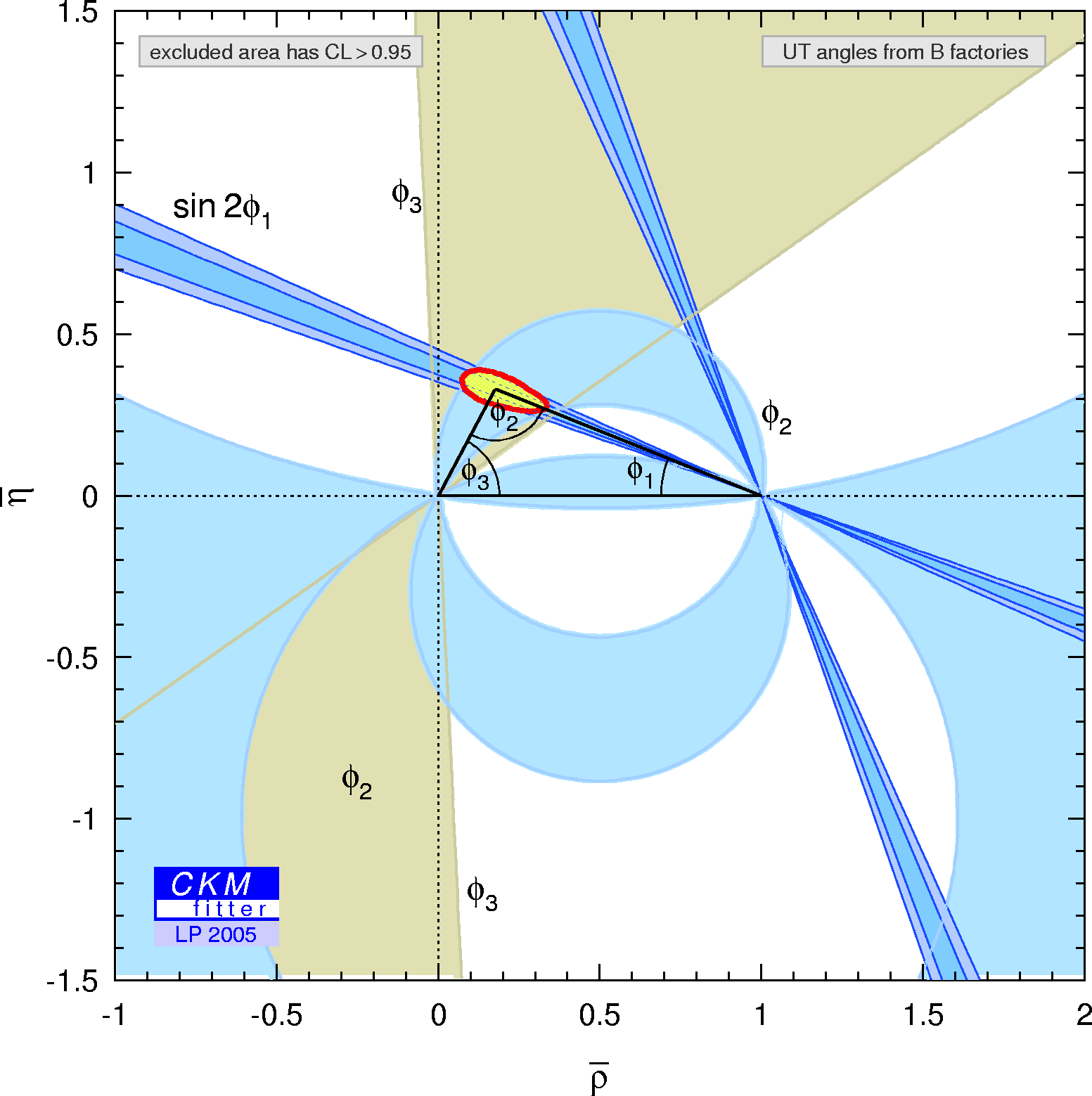eps gif
Constraints in the (ρ-bar,η-bar) plane including only the angle measurements in the global fit, and also showing the 3σ contours of the fit.	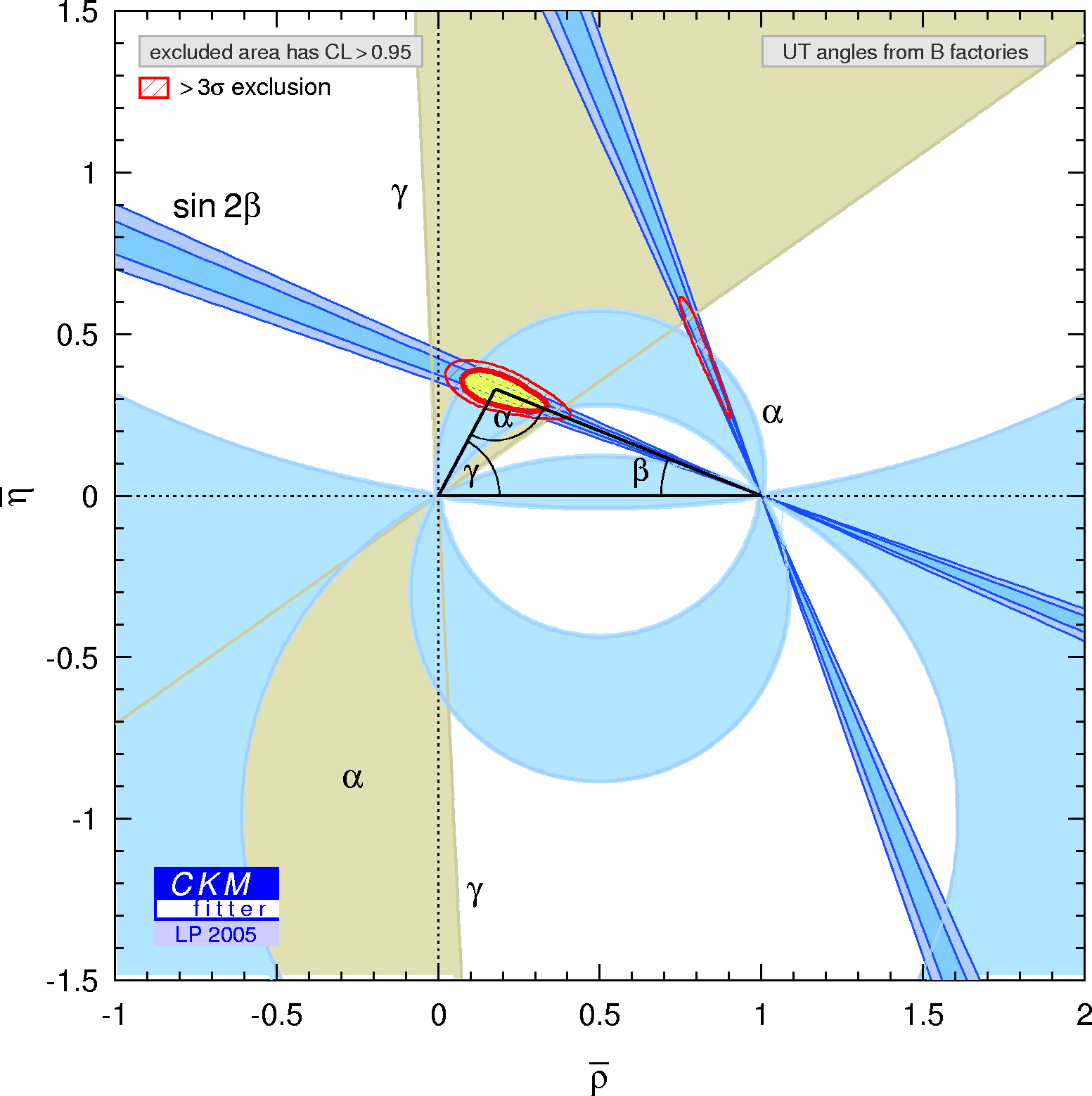eps gif	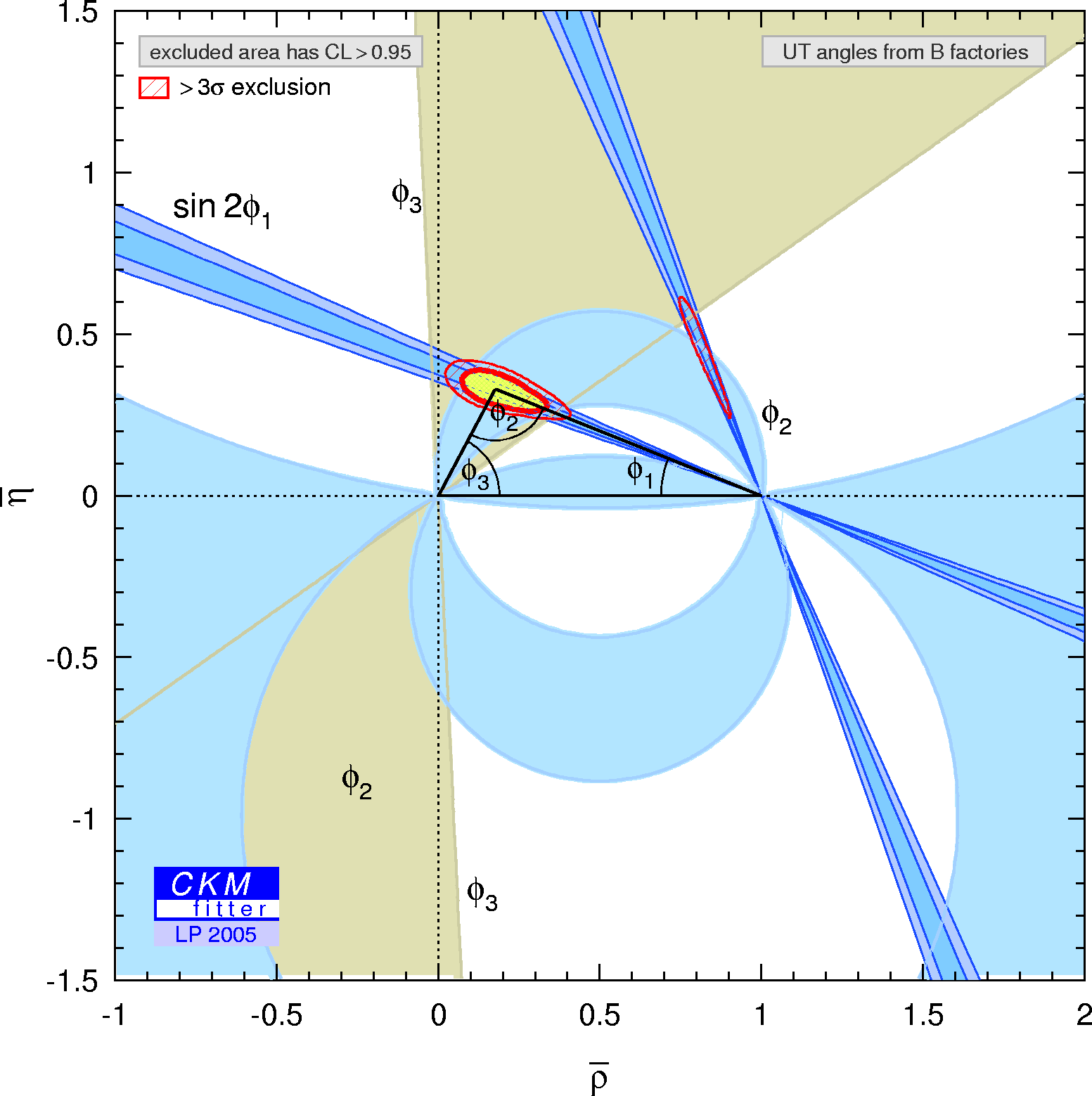eps gif

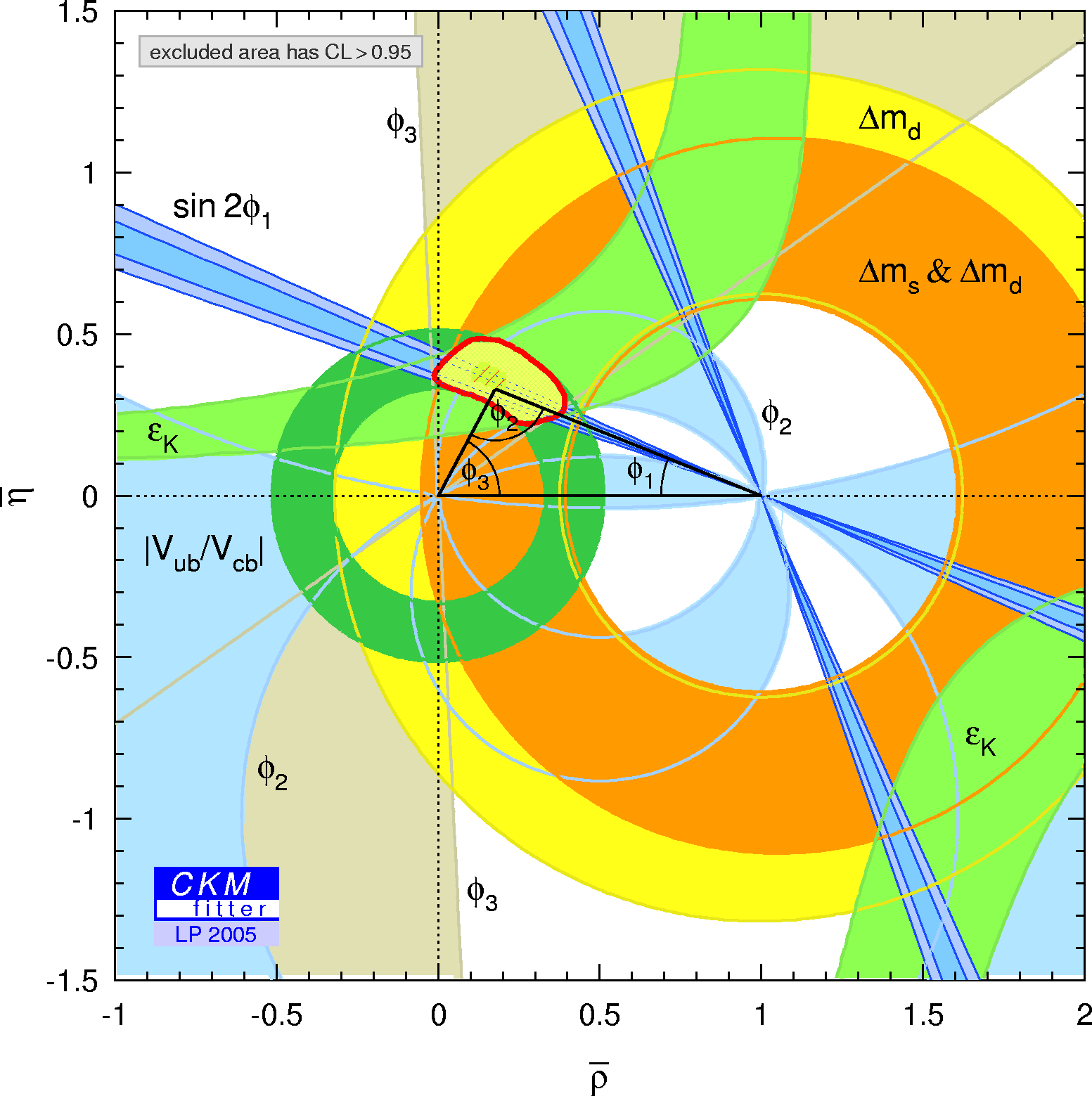
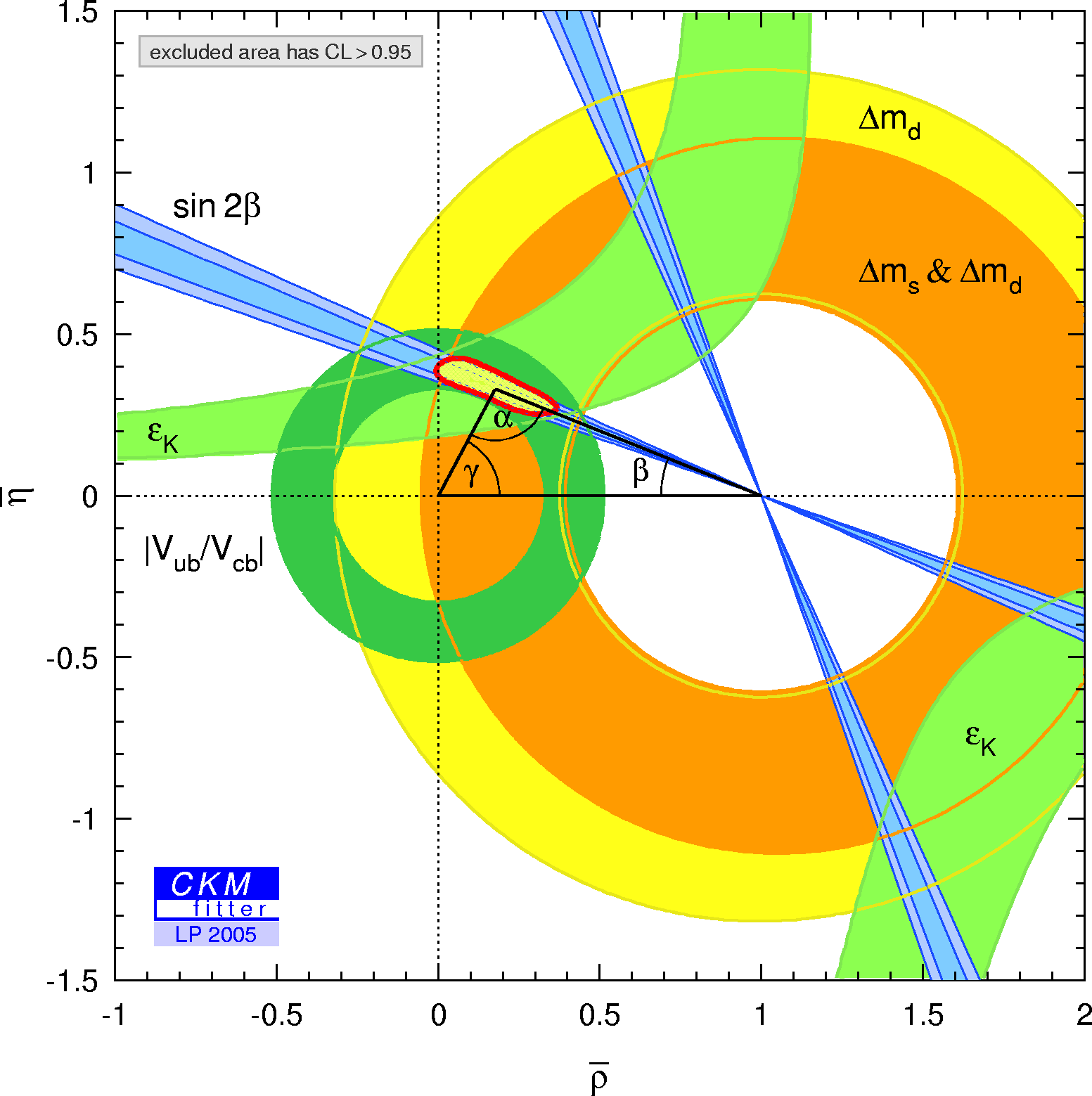
The global CKM fit in the small (ρ-bar,η-bar) plane (zoom):

	α,β,γ convention:	φ₁,φ₂,φ₃ convention:
Zoomed constraints in the (ρ-bar,η-bar) plane including the most recent α/Φ₂- and γ/Φ₃-related inputs in the global CKM fit.	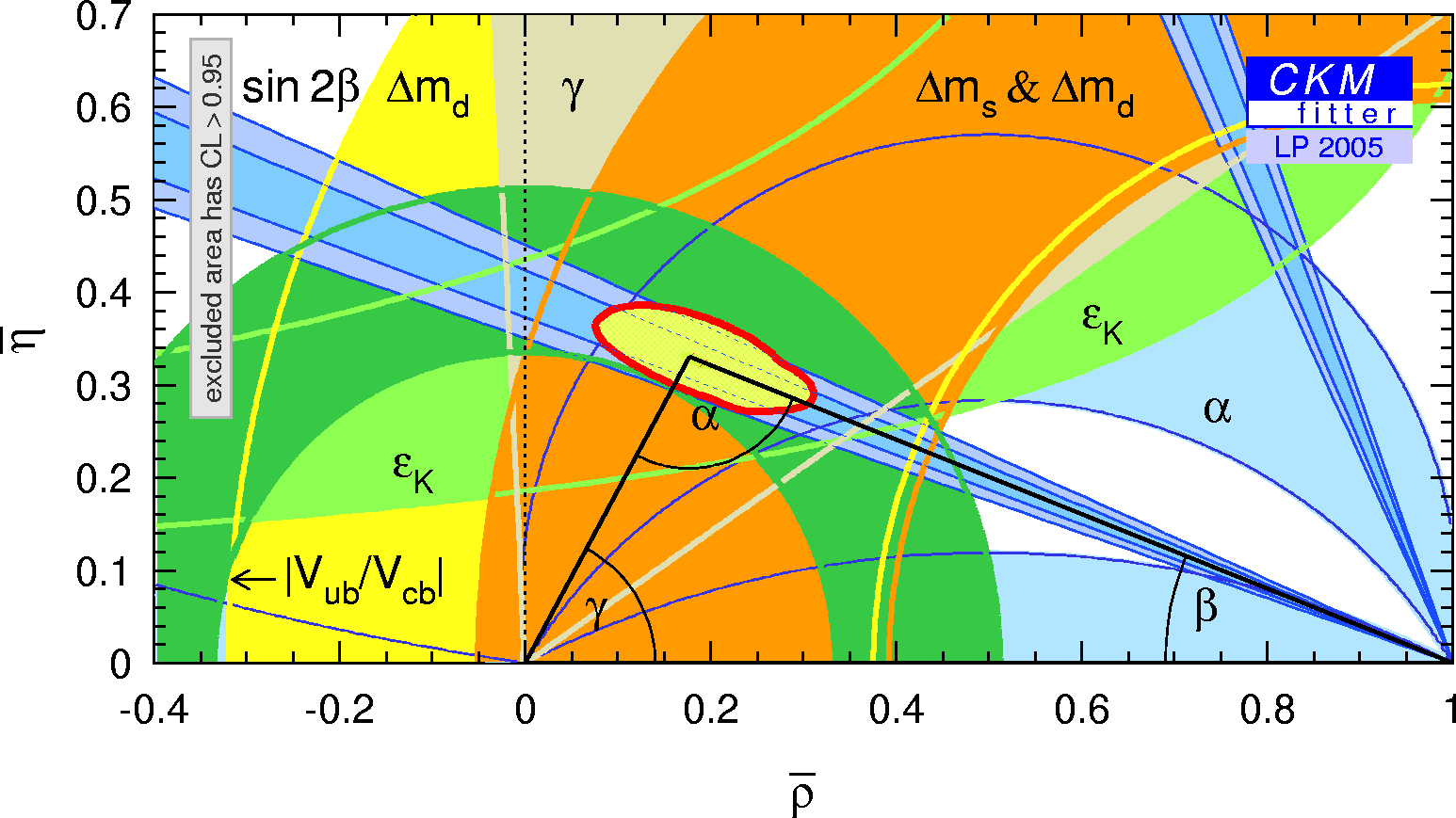eps gif	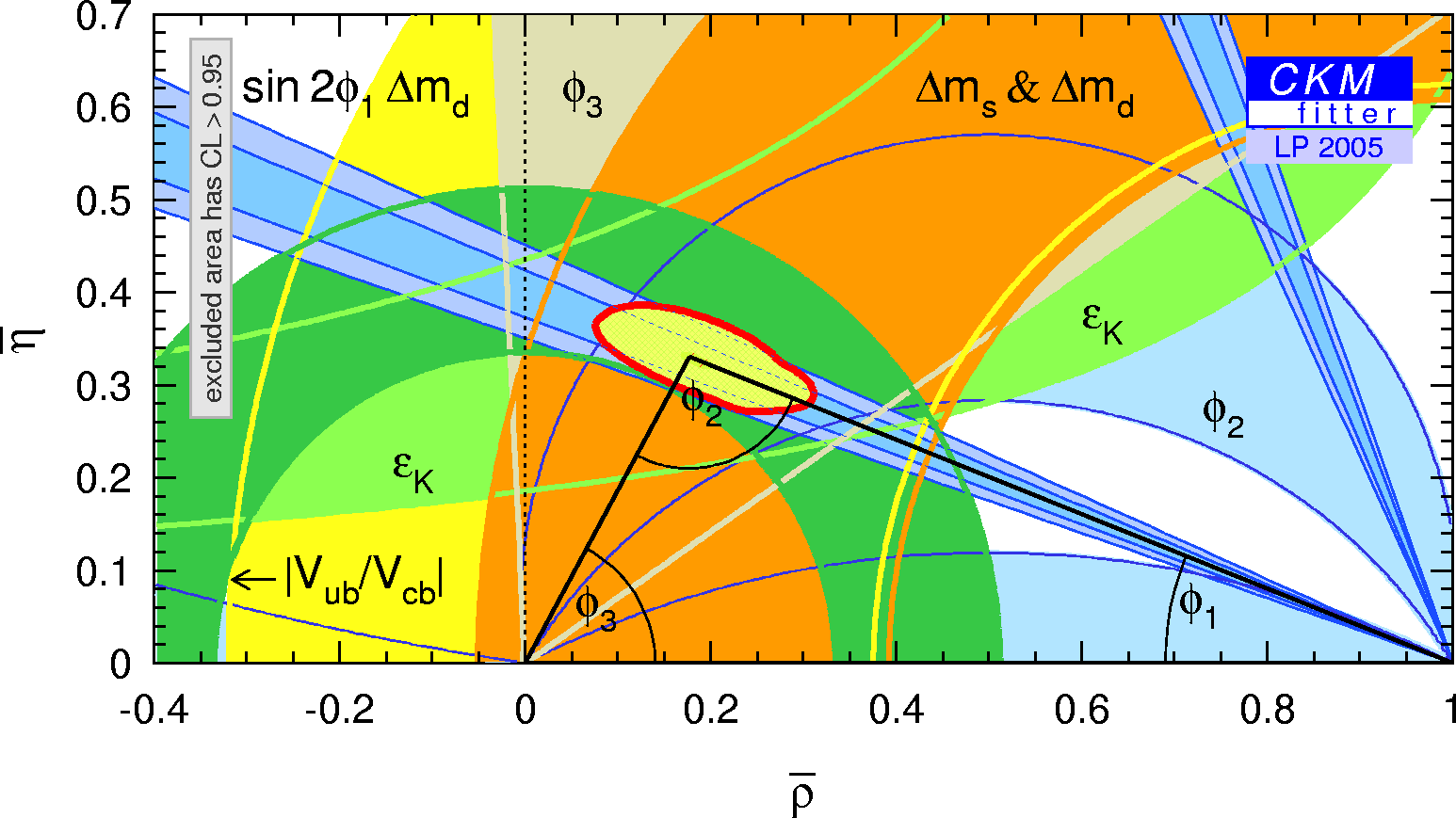eps gif
Zoomed constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit.	eps gif	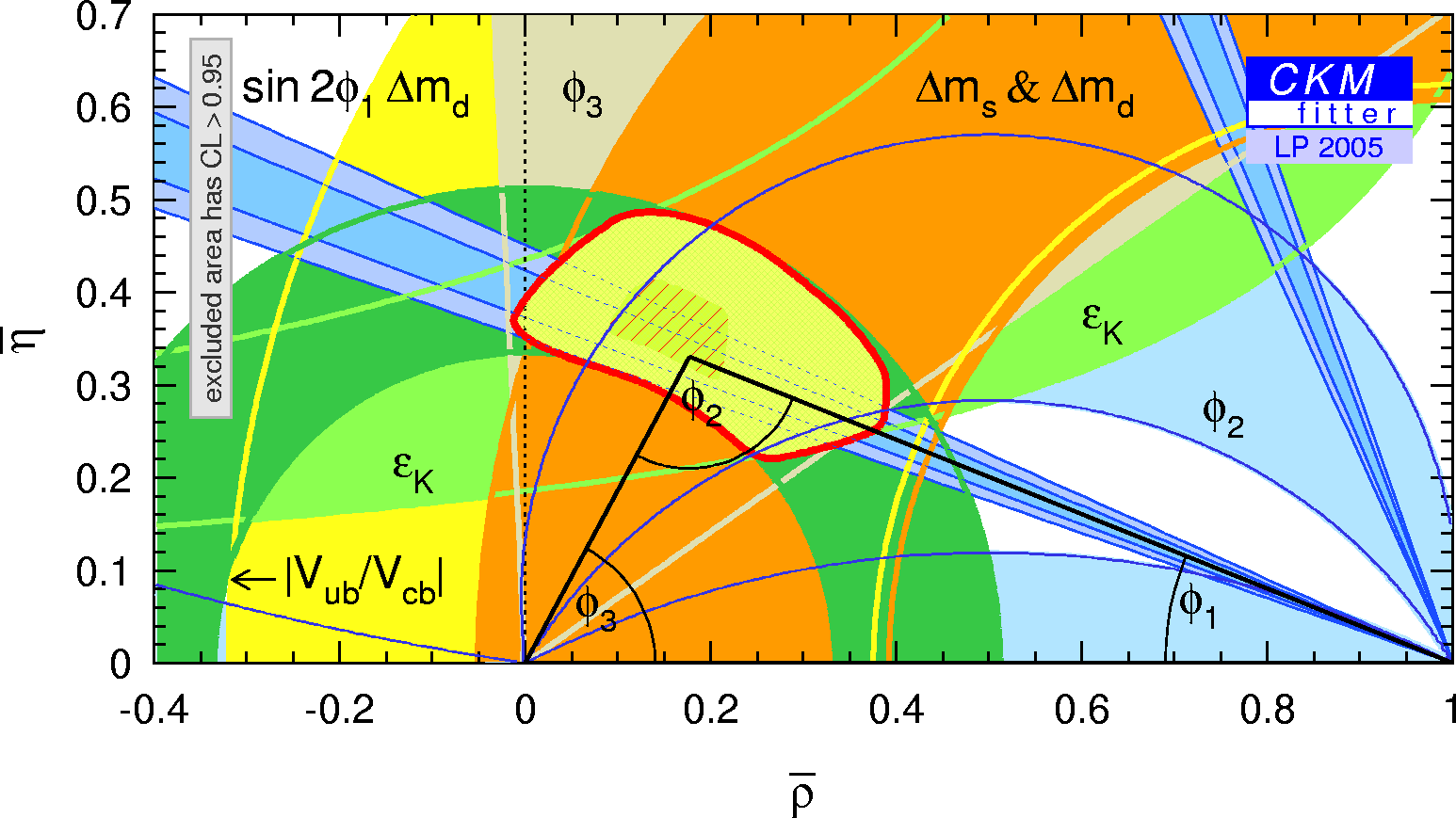eps gif
Constraints in the (ρ-bar,η-bar) plane including only the angle measurements in the global fit.	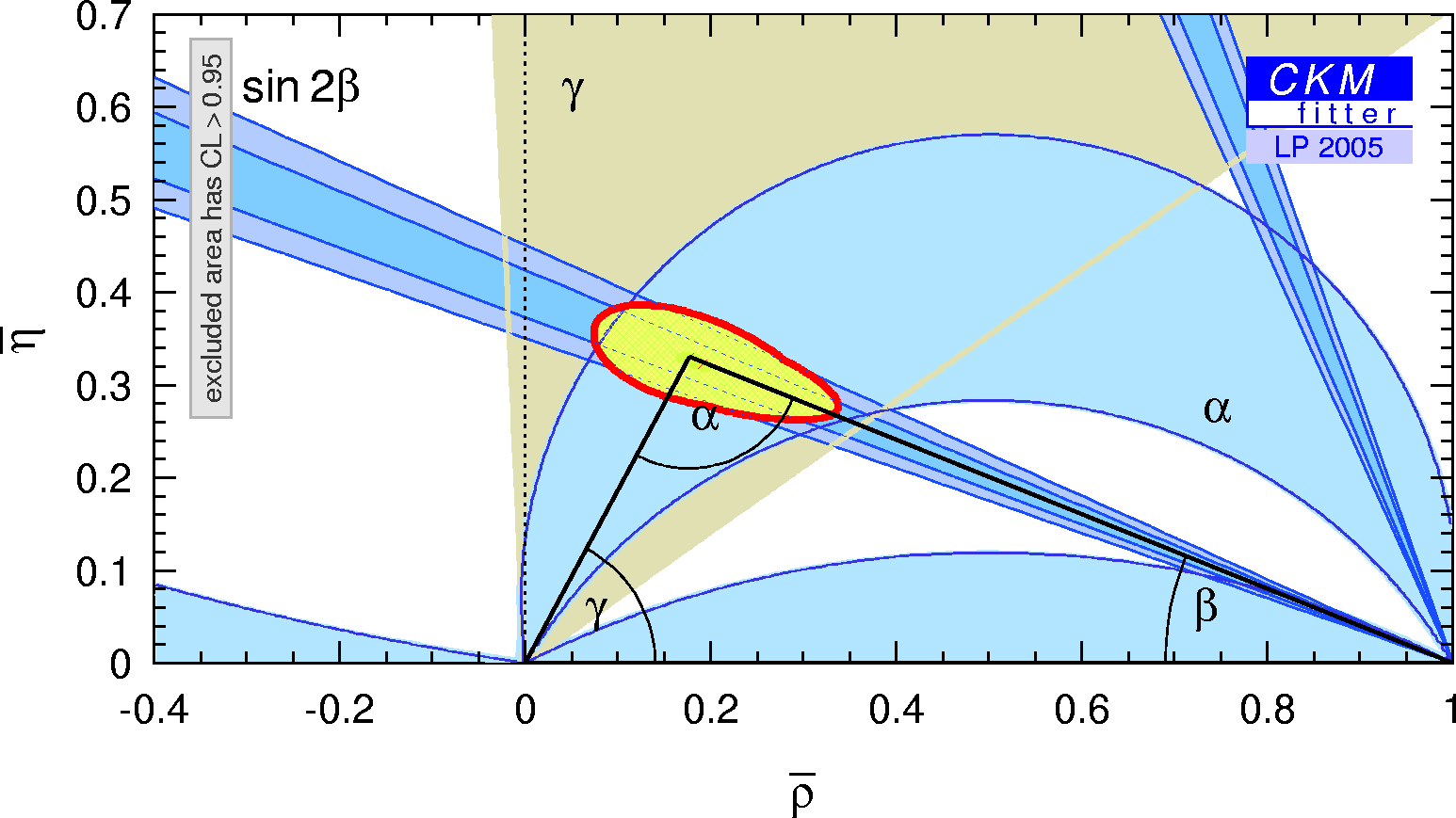eps gif	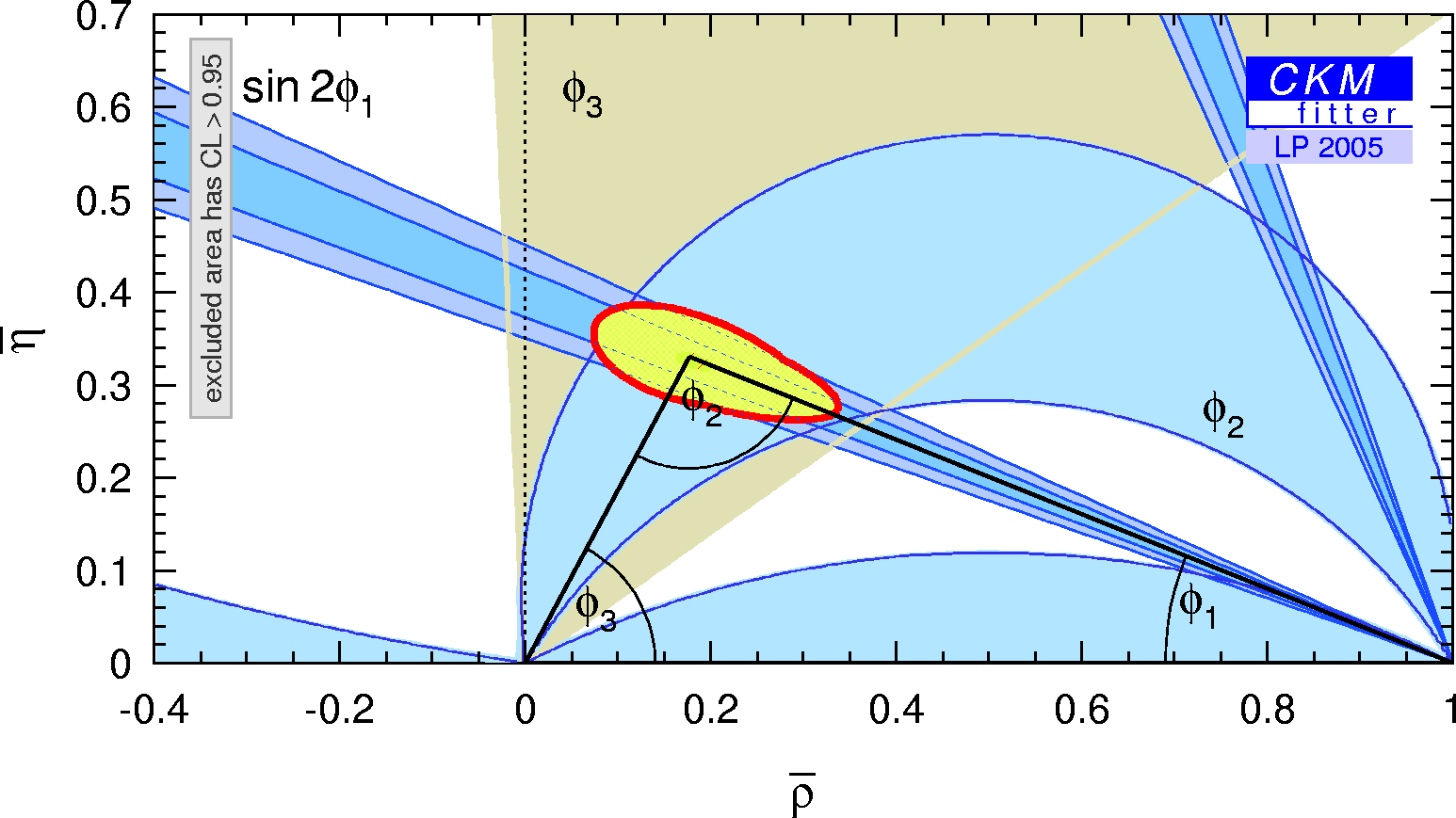eps gif

Constraints on the angle α/Φ₂ from charmless B decays:

Constraint on α/Φ₂ from B→ρρ.	eps gif
Constraints on α/Φ₂ from B→ππ, ρπ, ρρ, compared to the prediction from the CKM fit (not including these measurements). α[combined] = 99 +12/–9 deg.	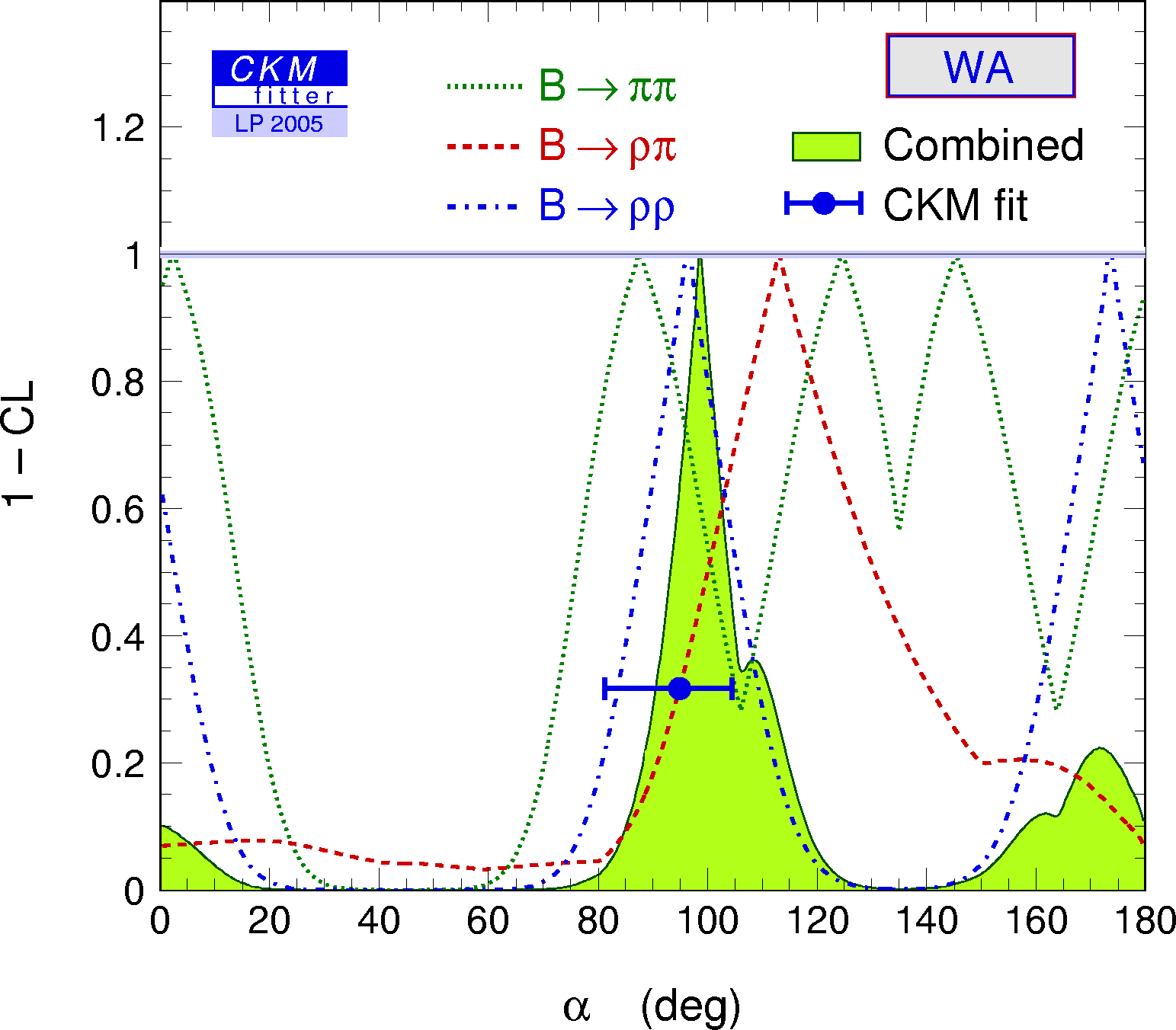eps gif
Constraint in the (ρ-bar,η-bar) plane from B→ππ, ρπ, ρρ, compared with the global CKM fit (not including these α-related measurements).	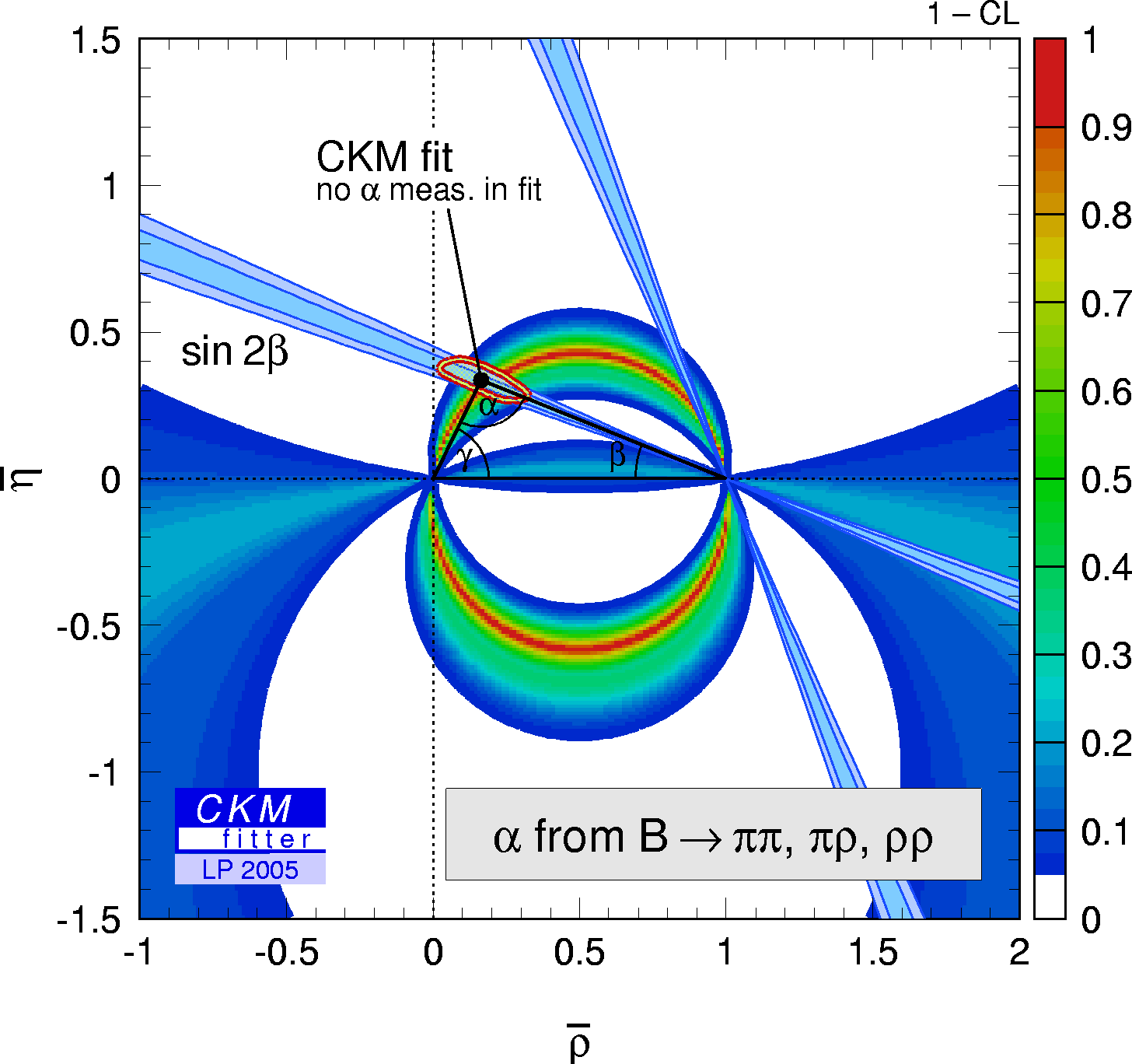eps gif

Constraints on the angle γ/Φ₃ from B decays to charm (to be updated):

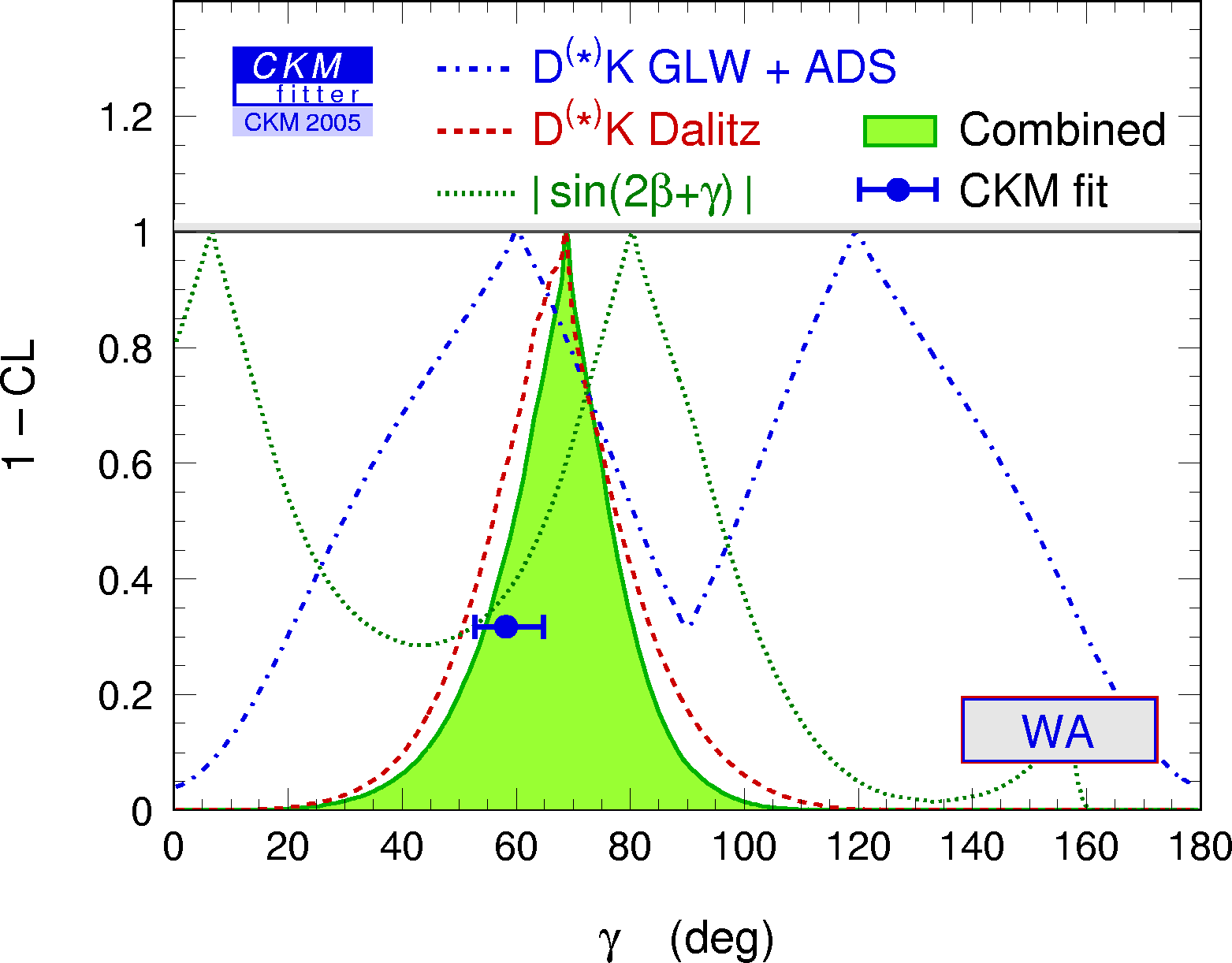
Constraints on γ/Φ₃ from D(*)K decays (GLW+ADS and Dalitz analyses) compared to the prediction from the global CKM fit (not including these measurements).
γ[GLW+ADS+GGSZ] = 63 +15 / –13°

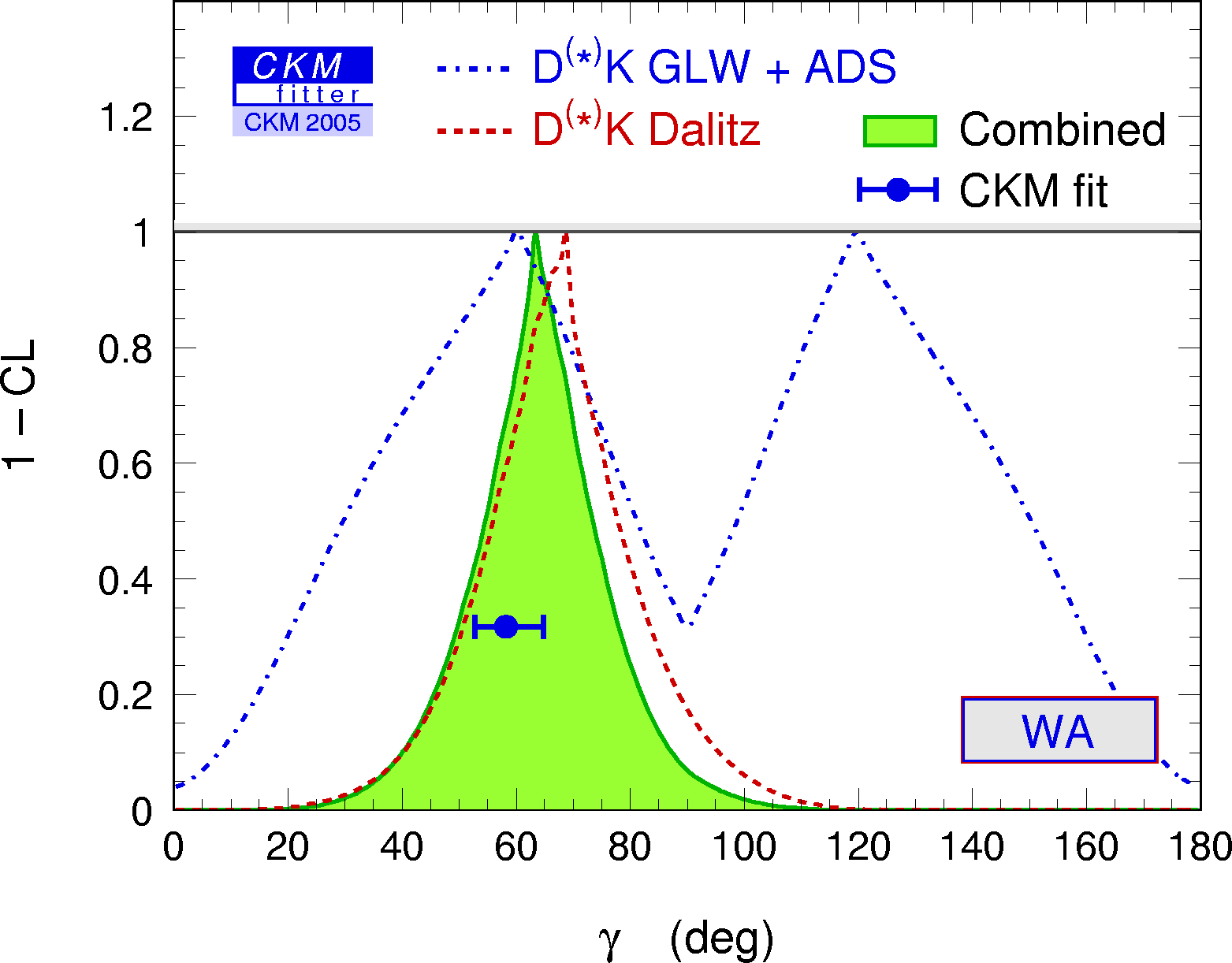eps gif

Constraints on the angle β_s (= δγ):

Constraints on the angle β_s =arg(-V_tsV_tb/V_csV_cb) (upper plot) and sin(2β_s) (lower plot) from the global CKM fit (no direct measurement from the time-dependent CP asymmetry in B⁰→J/ψφ decays is available yet). The numerical results for these quantities are given in the 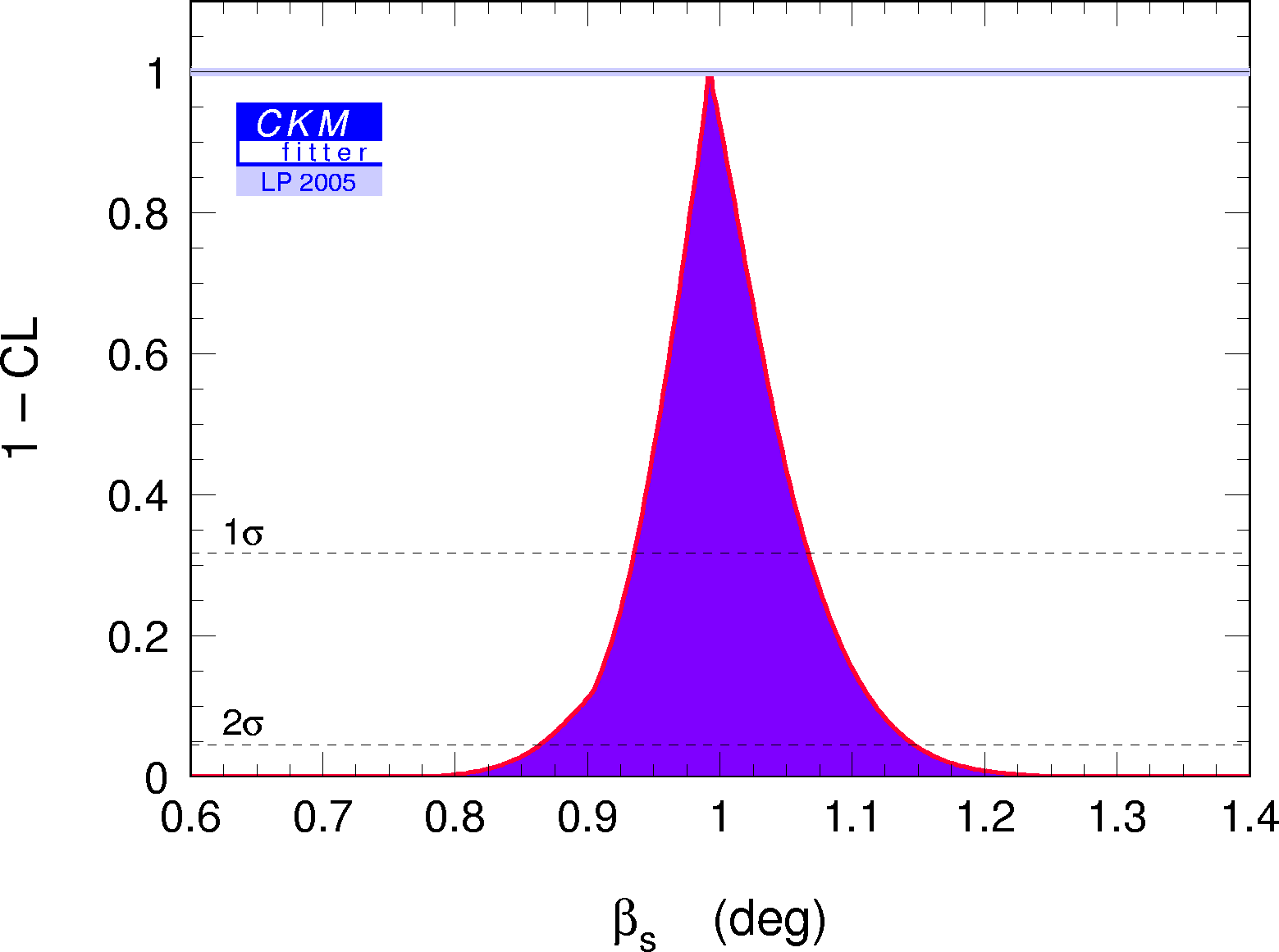summary paper.	eps gif
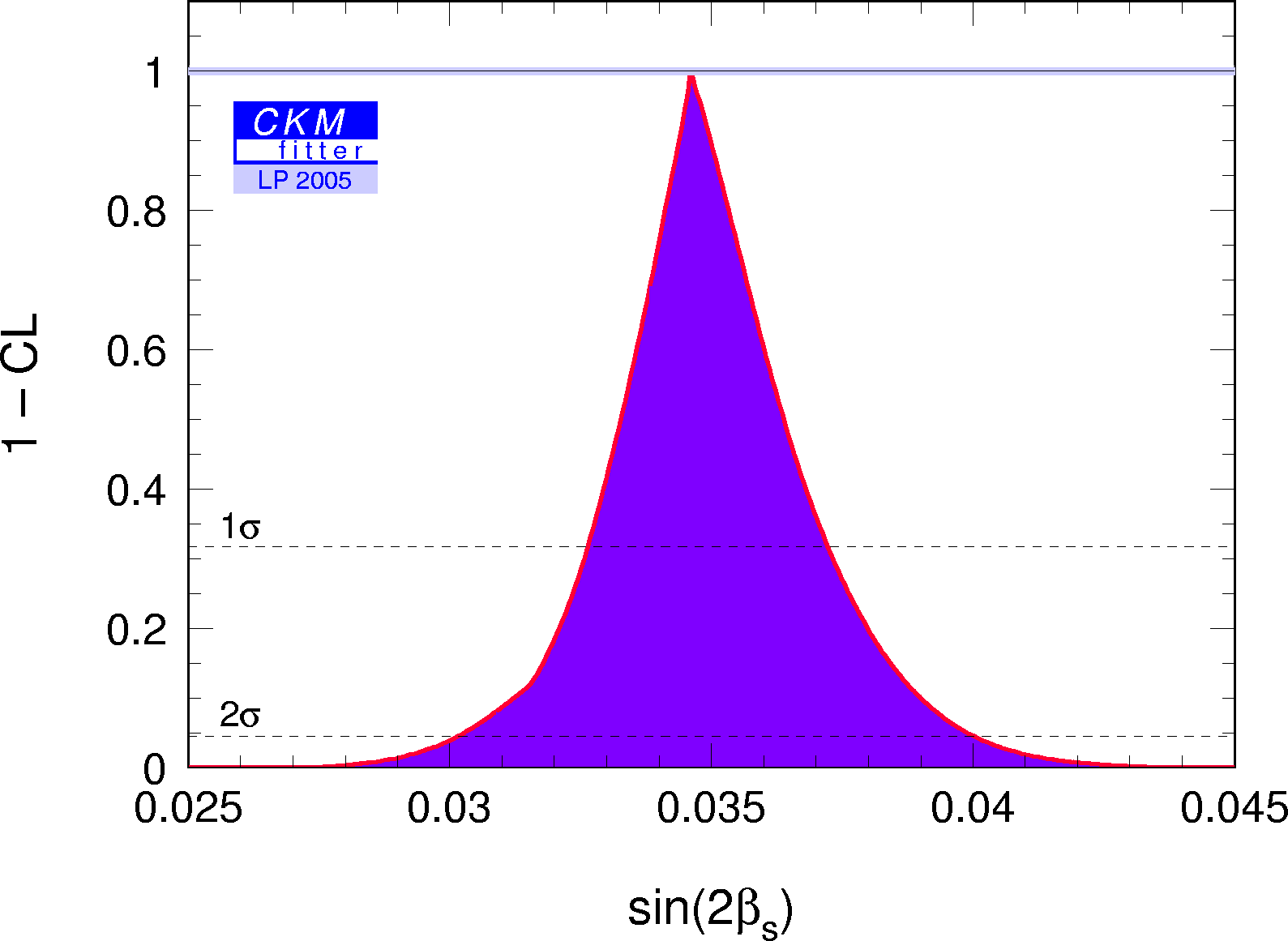	eps gif

Constraint from limit on the B⁺→τ⁺ ν branching fraction:

Constraint in the (ρ-bar,η-bar) plane from the simultaneous use of the limit on the B⁺→τ⁺ν branching fraction and Δm_d.	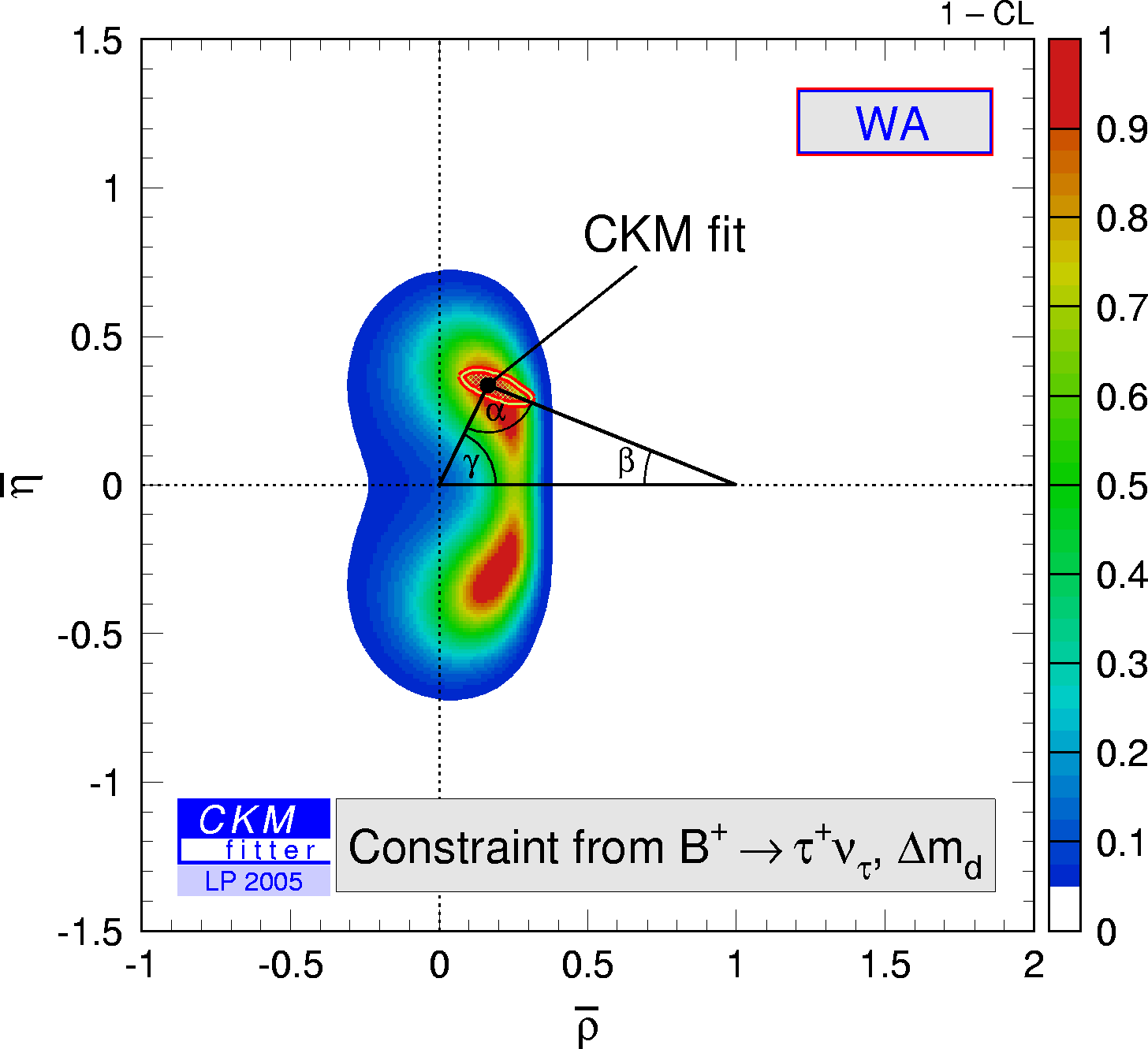eps gif
Constraint in the (ρ-bar,η-bar) plane from the simultaneous use of the limit on the B⁺→τ⁺ν branching fraction and Δm_d (Babar only).	eps gif

Constraint from b→d penguins:

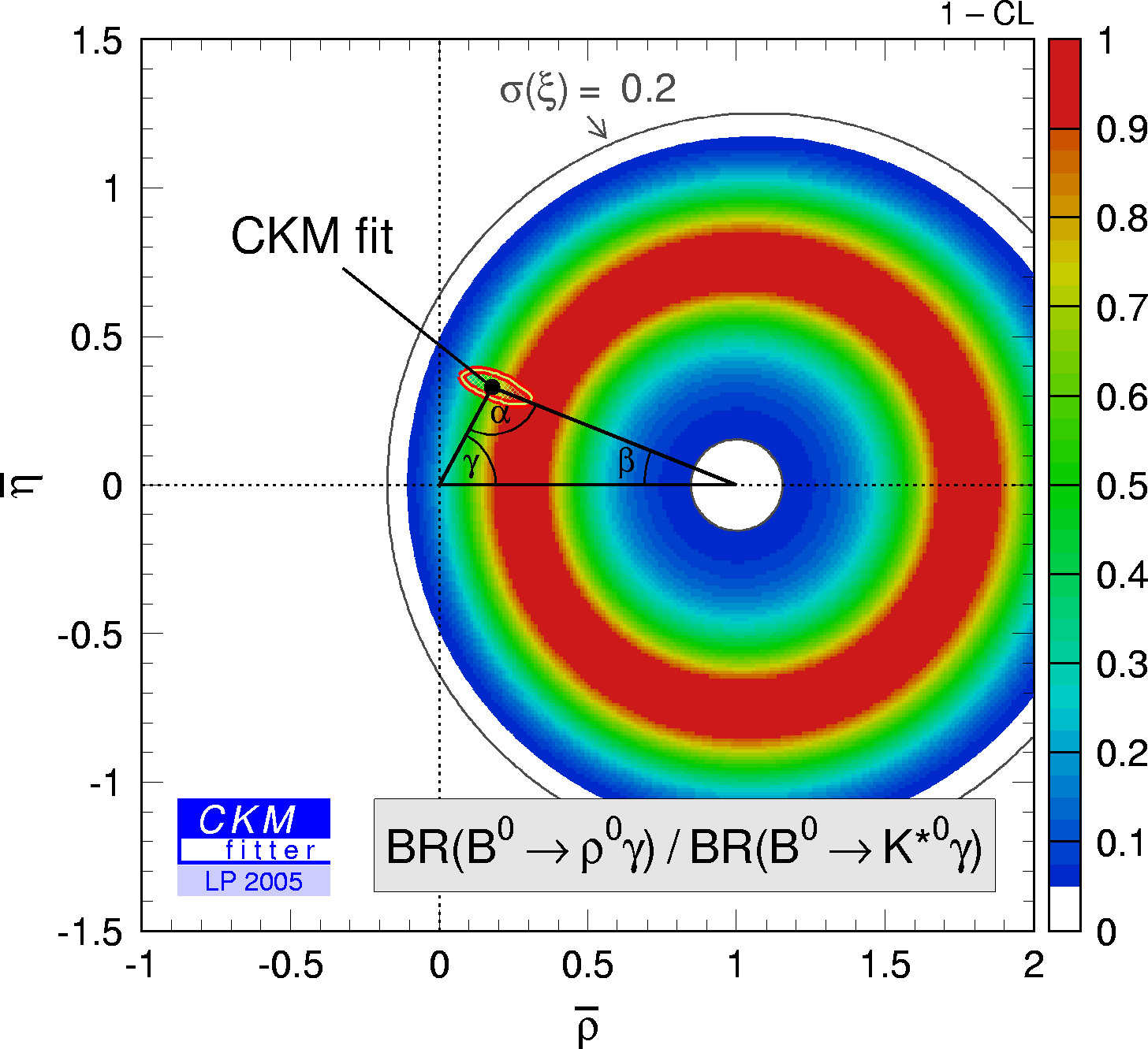
Constraint in the (ρ-bar,η-bar) plane from the branching fraction (B⁰→ρ⁰ γ / B⁰→K^*0 γ). Average BABAR and Belle.	eps gif
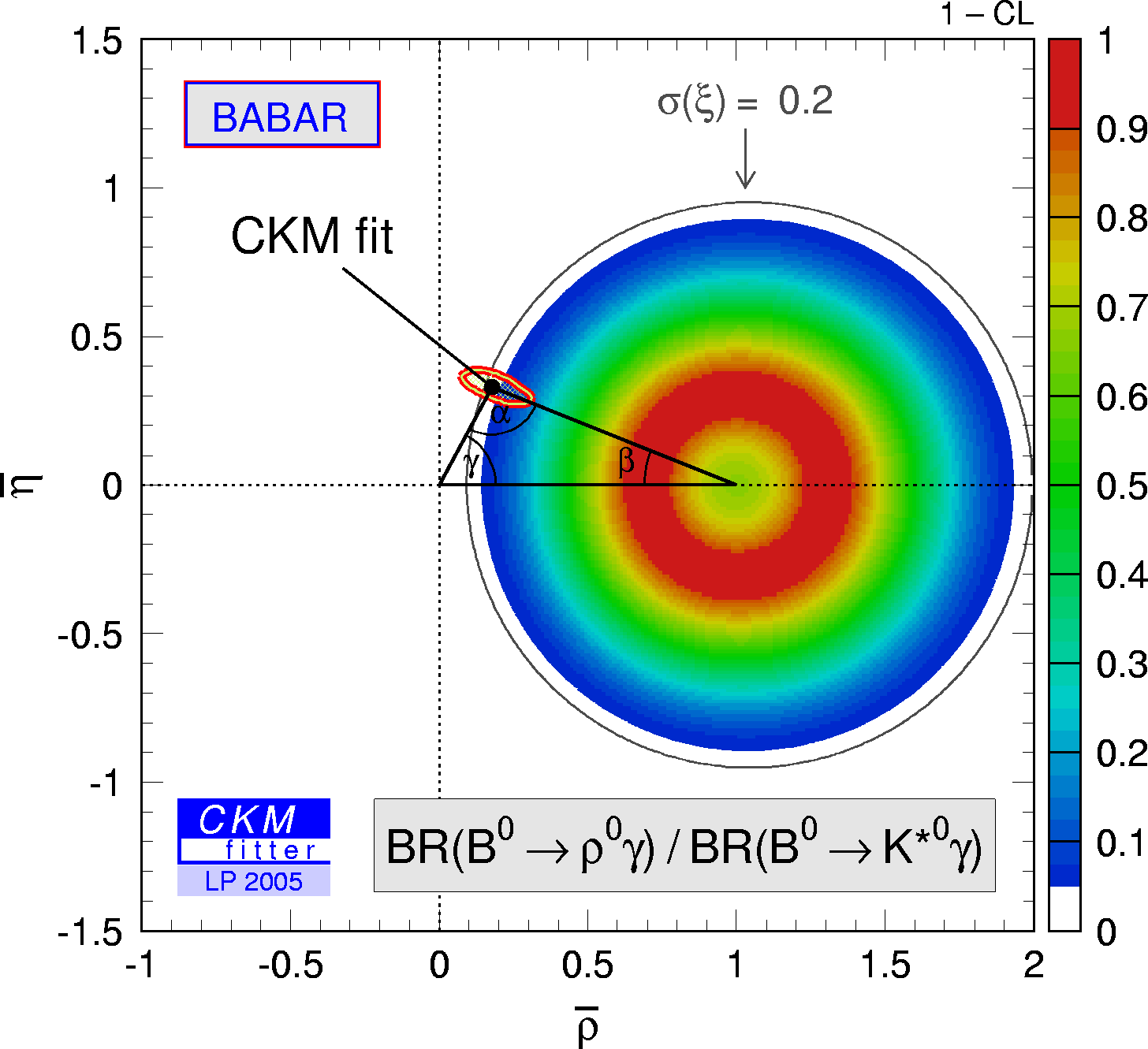
Constraint in the (ρ-bar,η-bar) plane from the branching fraction (B⁰→ρ⁰ γ / B⁰→K^*0 γ). BABAR only.	eps gif
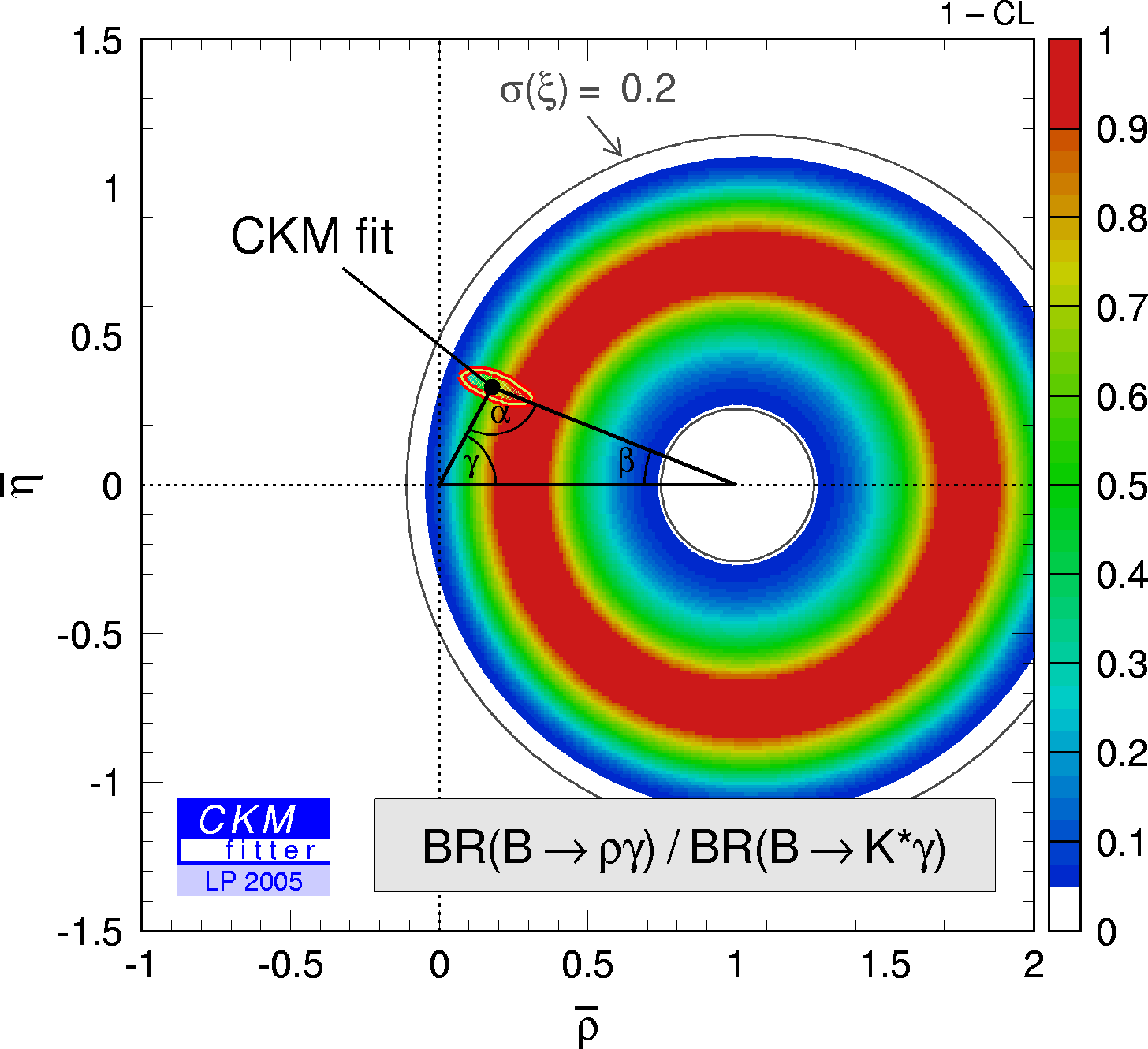
Constraint in the (ρ-bar,η-bar) plane from the ratio of the branching fractions (B→ργ / B→K^* γ) where the average of neutral and charged B decays (and average of BABAR and Belle) has been used.	eps gif

Constraints on |sin(2β+γ)|:

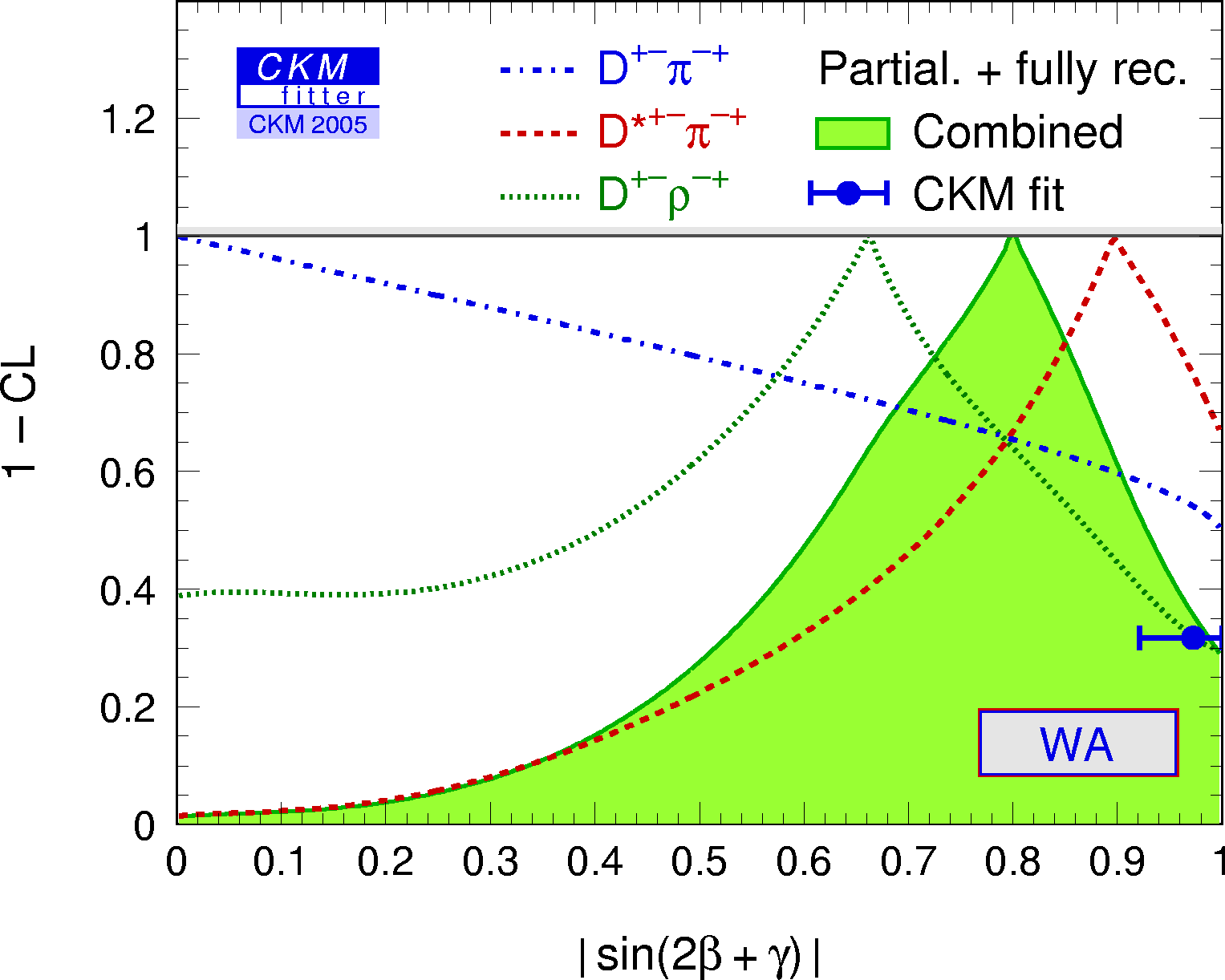
Constraints on \|sin(2β+γ)\| from the measurement of time-dependent CP asymmetries in D^() π (ρ). Moriond05 HFAG average is used as input. The extraction of the UT angles relies on SU(3) symmetry for the estimates of the suppressed-to-leading amplitude ratios. We use r = 0.019 ± 0.004 and r^ = 0.015 + 0.004 / – 0.006 , and apply an additional theoretical uncertainty in form of a 30% error range to these.	eps gif
Translation of this result into γ (using sin(2β) as additional input and choosing among the four solutions to the SM one). γ[GLW+ADS+GGSZ+\|sin(2β+γ)\|] = 70 +12 / – 14°	eps gif
Constraints from \|sin(2β+γ)\| in the (ρ-bar,η-bar) plane.	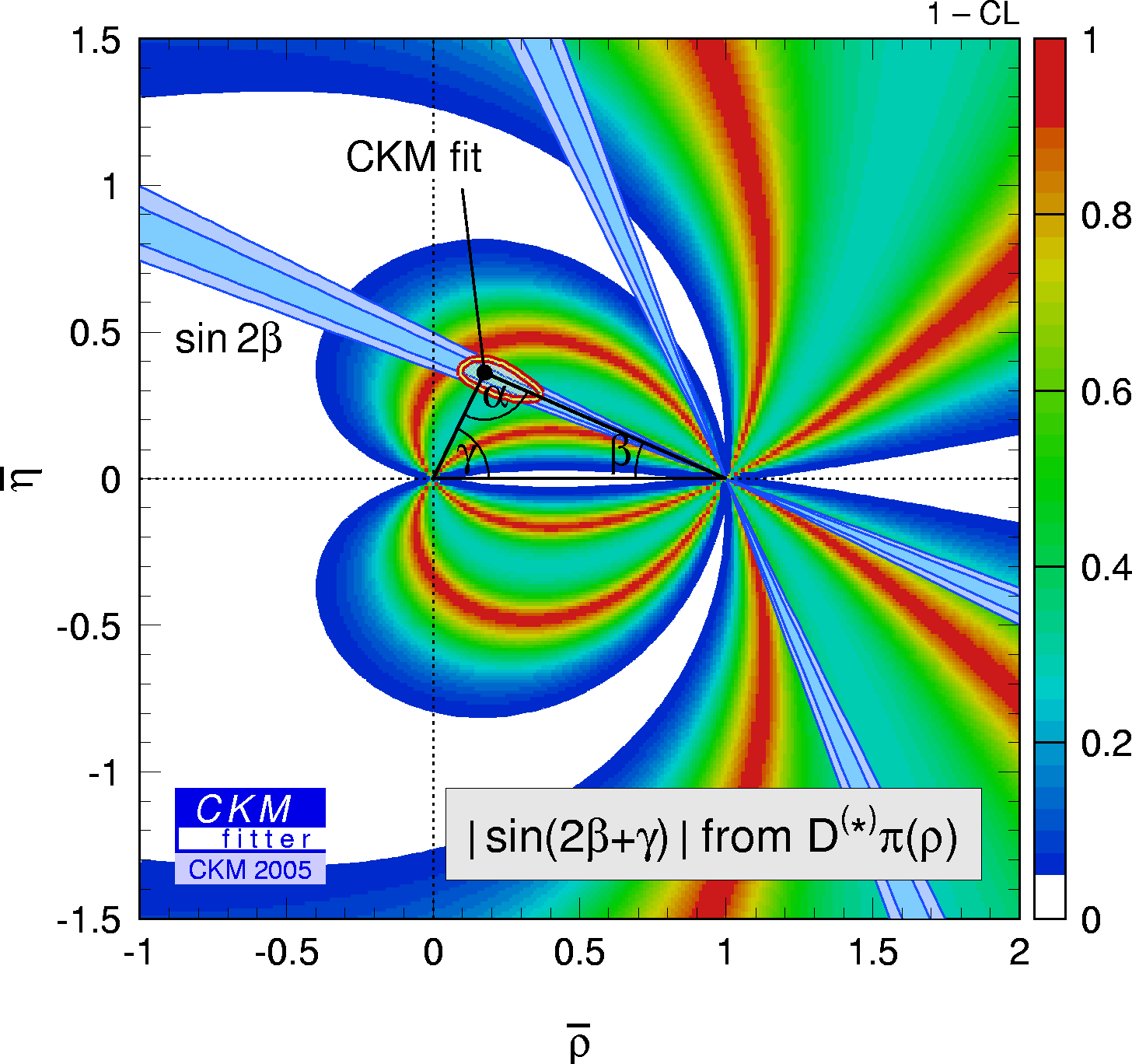eps gif

Contribution of the different input measurement families
to the constraint in the (ρ-bar,η-bar) plane (to be updated):

Constraints from CP conserving quantities (\|V_ub / V_cb\|, Δm_d, (Δm_d and Δm_s) and B⁺→τ⁺ ν) in the (ρ-bar,η-bar) plane.	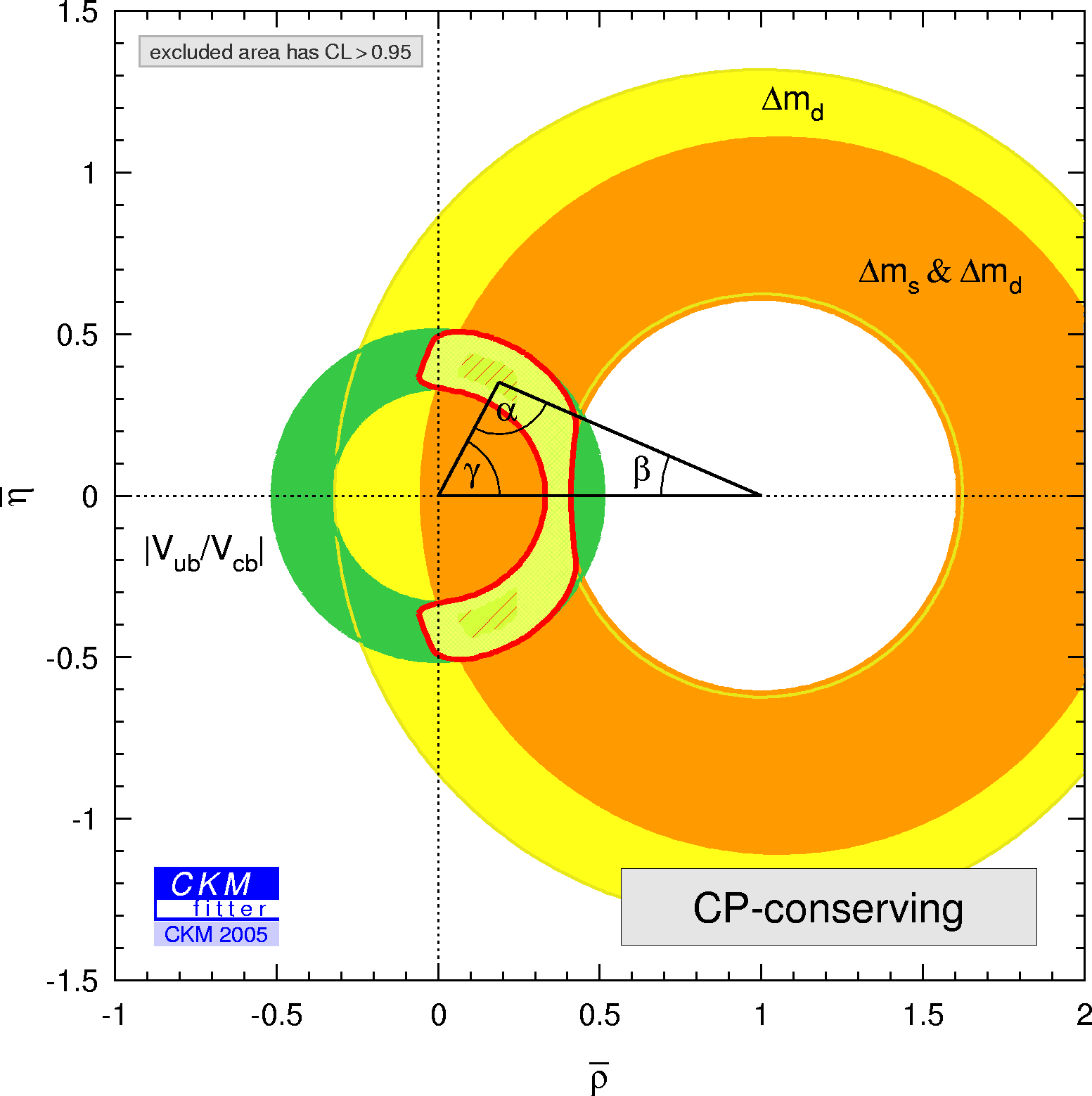eps gif
Constraints from CP violating quantities (sin(2β), α, γ and ε_k) in the (ρ-bar,η-bar) plane.	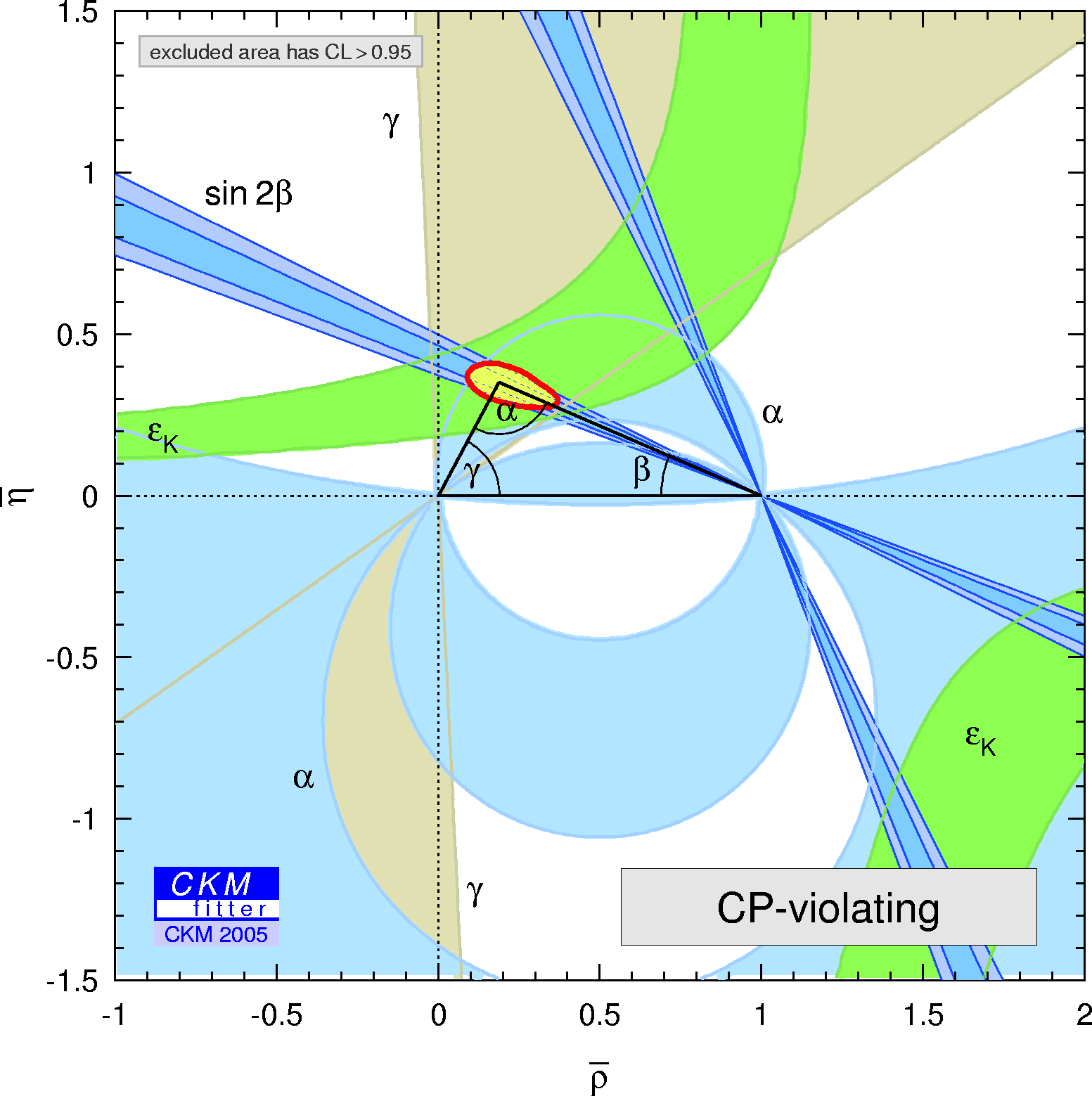eps gif
Constraints from \|V_ub / V_cb\| and s to d transition in the (ρ-bar,η-bar) plane.	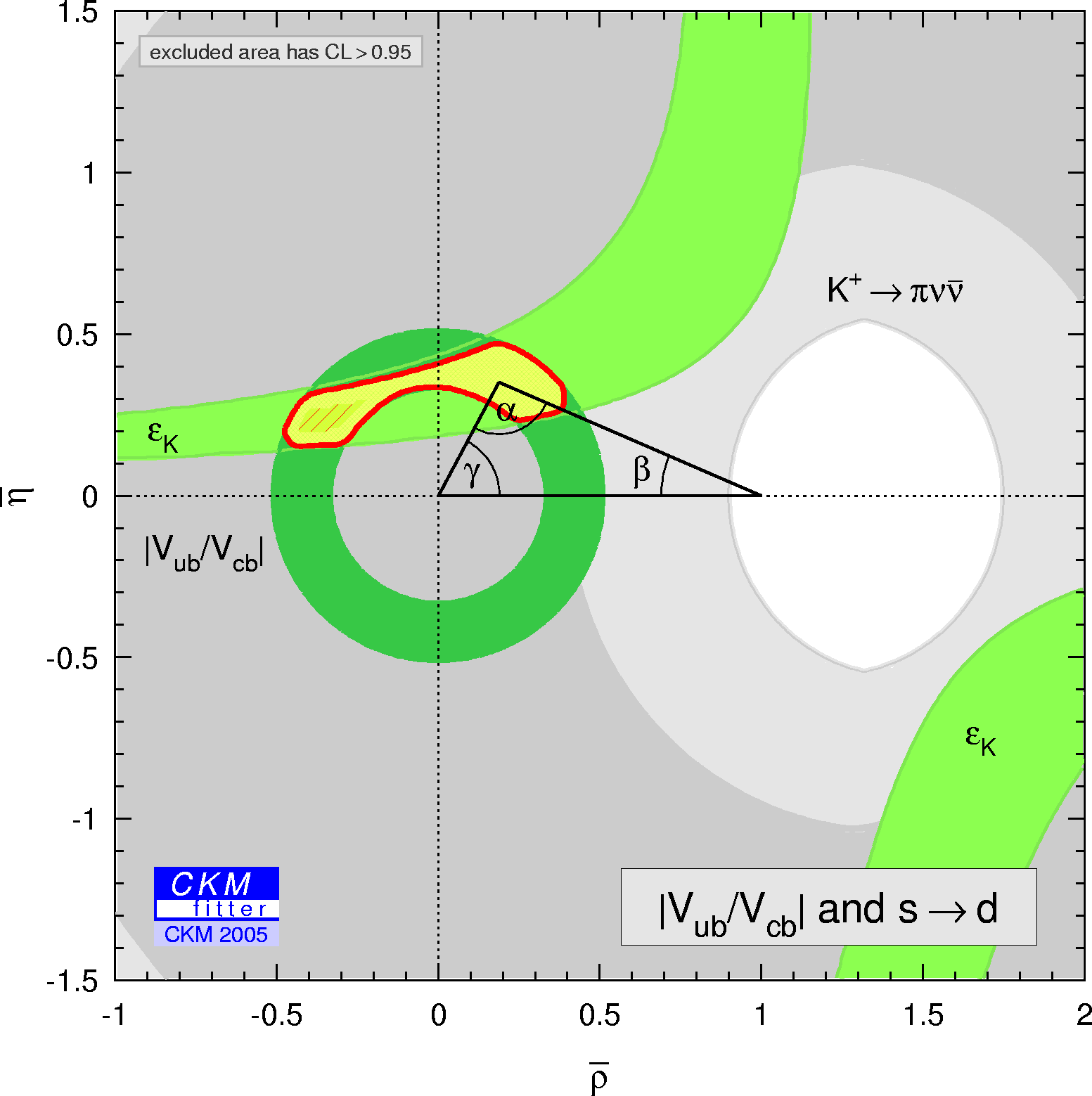eps gif
Constraints from \|V_ub / V_cb\| and b to d transition in the (ρ-bar,η-bar) plane.	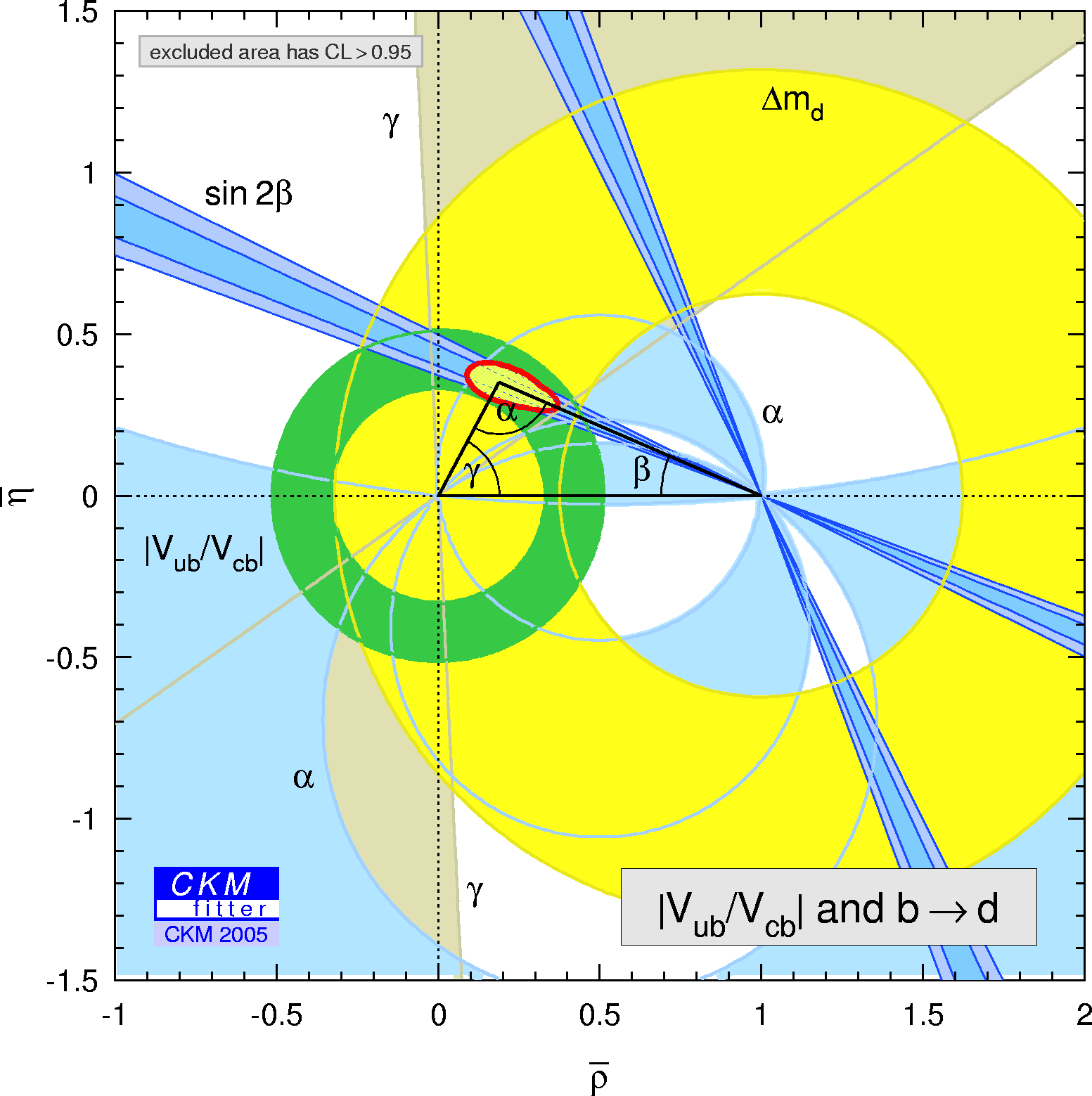eps gif
Constraints from \|V_ub / V_cb\| and b to s transition in the (ρ-bar,η-bar) plane.	eps gif

New physics in B⁰- B⁰bar Mixing (to be updated):

New physics in B⁰- B⁰bar Mixing can be described model-independently by introducing two new parameters measuring the relative strength (r_d²) and the relative phase between the B⁰- B⁰bar mixing matrix element containing contributions from SM as well as from NP contributions compared to SM contributions only:

r_d² * exp(i 2*Θ_d) =

<B⁰ | H[full] | B⁰-bar>
-------------------------------
<B⁰ | H[SM] | B⁰-bar>

Constraints from |V_cb| + |V_ub| , Δm_d=Δm_d^{SM} * r_d² and sin(2β+2Θ_d) in the (ρ-bar,η-bar) plane.

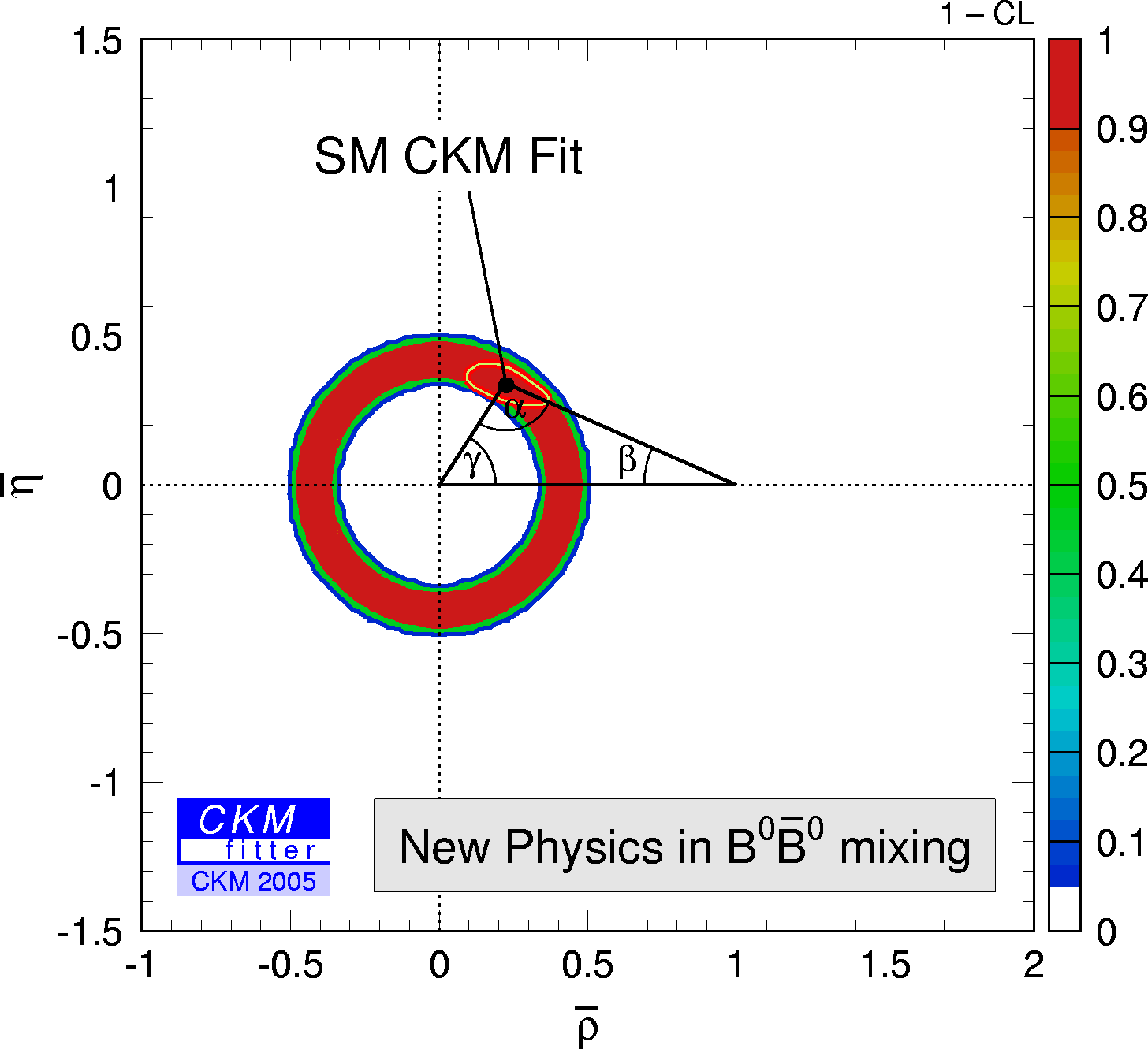eps gif

Constraints from |V_cb| + |V_ub| , Δm_d=Δm_d^{SM} * r_d² and sin(2β+2Θ_d) in the (2Θ_d , r_d²) plane.

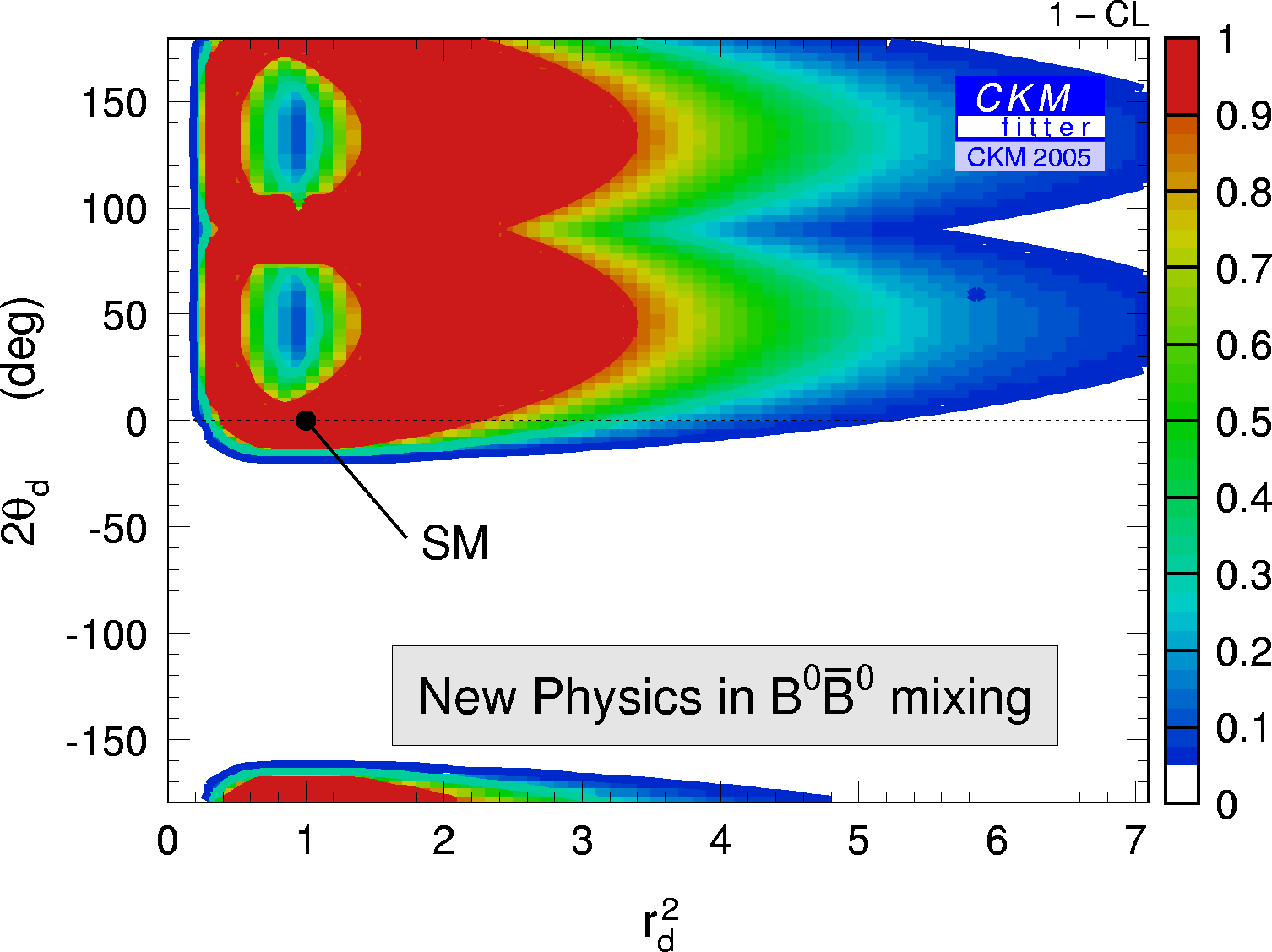eps gif

Since there are four free parameters in the fit (ρ-bar,η-bar,2*Θ_d,r_d²) but only three constraints depend on those there is no other constraint in the (ρ-bar,η-bar) plane visible but the one coming from |V_ub| and |V_cb| alone. As a consequence, the allowed region in the (2*Θ_d,r_d²) plane is large.

When using in addition the following inputs:
cos(2β) > 0 (suggested by data), α (ππ, 3π, ρρ), γ the allowed regions are substantially reduced:

in the (ρ-bar,η-bar) plane.

eps gif

in the (2*Θ_d,r_d²) plane.

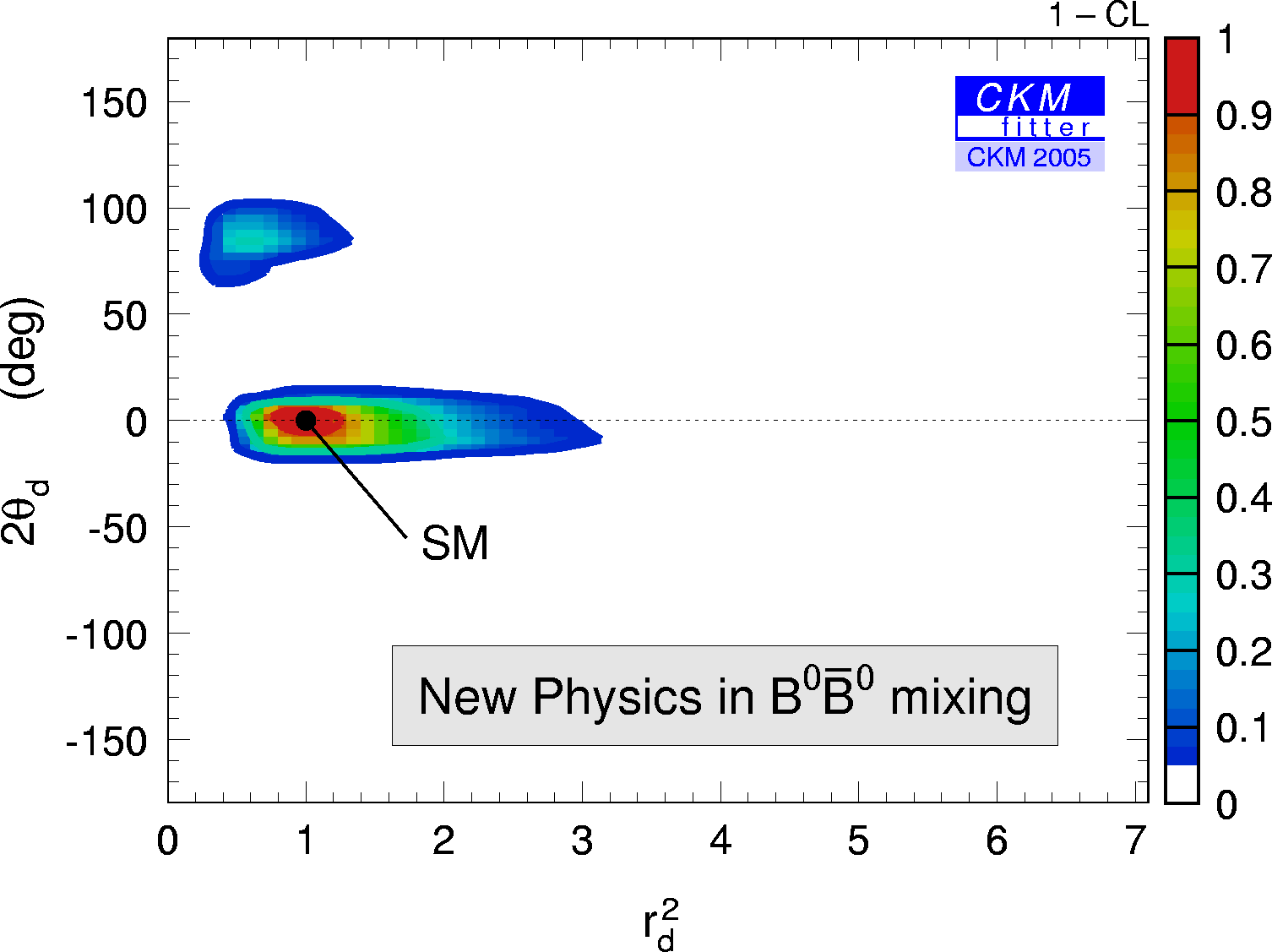eps gif

There are two solutions left. The SM solution (2*Θ_d = 0 ,r_d² = 1) is prefered. If the other solution can be eliminated with more data the possible additional phase from NP could not be very large (<15 degree). The relative strength of NP to SM contributions can still easily be of order 100%.