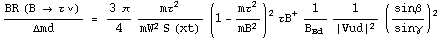CKMfitter

Preliminary results as of Winter 2012
(Moriond conference)

Menu:

The global CKM fit: Inputs and Numerical results

The global CKM fit in the large (ρ-bar,η-bar) plane

The global CKM fit in the large (ρ_s-bar,η_s-bar) plane

Branching ratio of B_s→μ⁺ μ^-

New physics in neutral-meson mixing

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom)

The global CKM fit in the (|V_ud|,|V_us|) plane

Constraint from BR(B⁺→τ⁺ ν)

Constraint from decays B→ V γ

Constraints on the angle α/ϕ₂ from charmless B decays

Constraints on the angle γ/ϕ₃ from B decays to charm

Constraints on |sin(2β+γ)|

Numerical results:

The results of the global CKM analysis include:

Wolfenstein parameters,
UT angles and sides,
UT_sangle and apex,
CKM elements,
theory parameters,
rare branching fractions (B->lν, B->ll).

Numerical Results

The global CKM fit in the large (ρ-bar,η-bar) plane:

Constraints in the (ρ-bar,η-bar) plane. The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane. The |Vub| constraint has been splitted in the two contributions: |Vub| from inclusive and exclusive semileptonic decays (plain dark green) and |Vub| from B⁺→τ⁺ ν (hashed green). The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

The global CKM fit in the large (ρ_s-bar,η_s-bar) plane:

Constraints in the (ρ_s-bar,η_s-bar) plane. The red hashed region of the global combination corresponds to 68% CL. The (almost horizontal) thin blue lines correspond to the 68% and 95% CL constraints on β_s from the combined results on B_s->J/Ψφ from CDF [arXiv:1112.1726] and LHCb [arXiv:1112.3183].

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Branching ratio of B_s→μ⁺ μ^-

SM prediction for Br(B_s→μ⁺ μ^-)=(3.64^+0.21_-0.32)x10^-9.

eps png

New physics in neutral-meson Mixing

See the specific studies performed for the article New Physics in B-B mixing
in the light of recent LHCb data (here).

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom):

Zoomed constraints in the (ρ-bar,η-bar) plane.The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Zoomed constraints in the (ρ-bar,η-bar) plane. The |V_ub| constraint has been splitted in the two contributions: |V_ub| from inclusive and exclusive semileptonic decays (plain dark green) and |V_ub| from B⁺→τ⁺ ν (hashed green). The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Zoomed constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane including only the angle measurements.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from CP conserving quantities (|V_ub / V_cb|, Δm_d, (Δm_d and Δm_s) and B⁺ →τ⁺ ν) in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from CP violating quantities (sin(2β), α, γ and ε_k) in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from "Tree" quantities in the (ρ-bar,η-bar) plane (γ(DK) and α from the isospin analysis with the help of sin2β (charmonium), which gives another tree only γ measurement (the only assumption is that the ΔI=3/2 b-->d EW penguin amplitude is negligible)).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from "Loop" quantities in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane, not including the braching ratio of B⁺ → τ⁺ν in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane not including the measurement of sin2β in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

The global CKM fit in the (|V_ud|,|V_us|) plane:

No update

See Summer 11 results (here).

Constraint from the B⁺→τ⁺ ν branching ratio:

There is a discrepancy in the CKM global fit between the world averages for sin2β and BR(B→τν).

There is a specific correlation between the two quantities in the global fit that is a bit at odds with the direct experimental determination. This is best viewed in the (sin2β,BR(B→τν)) plane, regarding the prediction from the global fit without using these measurements. The cross corresponds to the experimental value with 1 sigma errors.

eps png

The shape of the correlation can be understood by considering the ratio BR(B→τν)/Δm_d, where the decay constant f_{B_d} cancels, leaving limited theoretical uncertainties (the ratio depends only on the bag parameter B_{B_d}). Thus from the observables BR(B→τν) and Δm_d one gets an interesting constraint in the (ρbar,ηbar) plane, which does not match perfectly with the global fit output.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

To have a closer look, one can write the full formula for the ratio

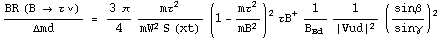
where one explicitly sees that the correlation between BR(B→τν) and the angle β is controlled by the values of B_{B_d}, and the angles α and γ. This can be checked explicitly by comparing the above analytical formula with the colored region in the (sin2β,BR(B→τν)) plane. In other words the discrepancy is not driven by the value of semileptonic |V_ub|, nor by the decay constant f_{B_d}.

To quantify the discrepancy one can compare the indirect fit prediction for BR(B→τν) with the measurement. The deviation here is 2.8 sigmas.

eps png

A simpler test is the comparison of the prediction of B_{B_d} from the above analytical formula (having only BR(B→τν), Δm_d, α, β, γ and |V_ud| as inputs, that is an almost completely theory-free determination of B_{B_d}) with the current lattice determination B_{B_d} = 1.262 ^+0.083_-0.081.

For this test the deviation is 2.9 sigmas, dominated by the error on BR(B→τν), α, γ and B_{B_d}.

eps png

Constraint from B → V γ decays

No update

See Summer 08 results (here).

Constraints on the angle α/ϕ₂ from charmless B decays

We have included LHCb results for C(ππ) and S(ππ) presented at Moriond 2012 as well as Belle results for BR(ππ) and BR(π⁺π⁰) presented at EPS2011. One observes a slight degradation of the accuracy for α due to the decrease of BR(π⁺π⁰) that weakens the degeneracy of mirror solutions, yielding: α[combined]= 88.7^+4.6_-4.2°.

Constraint on α/ϕ₂ from B→ππ compared to the prediction from the global CKM fit (not including the α-related measurements) α[fit]= 95.9^+2.2_-5.6°.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on α/ϕ₂ from B→ρπ (BABAR, Belle and WA) compared to the prediction from the global CKM fit (not including the α-related measurements).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on α/ϕ₂ from B→ρρ (BABAR, Belle and WA) compared to the prediction from the global CKM fit (not including the α-related measurements).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on α/ϕ₂ from the combination of B→ππ, ρπ, and ρρ for BABAR, Belle and WA, compared to the prediction from the global CKM fit (not including the α-related measurements).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on α/ϕ₂ from B→ππ, ρπ and ρρ (WA) compared to the prediction from the global CKM fit (not including the α-related measurements).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on the angle γ/ϕ₃ from B decays to charm

Constraints on γ/ϕ₃ from world average D(*)K(*) decays (GLW+ADS) and Dalitz analyses (GGSZ) γ[combined] = 66± 12°, compared to the prediction from the global CKM fit (not including these measurements): γ[fit] = 67.2^+4.4_-4.6°.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Illustration of the correlation between the determination of γ/ϕ₃ and the ratio of interfering amplitudes r_B of the decay B → DK from world average D(*)K(*) decays (GLW+ADS) and Dalitz analyses (GGSZ).

eps png

Constraint on the ratio of interfering amplitudes r_B of the decay B → DK from world average D(*)K(*) decays (GLW+ADS) and Dalitz analyses (GGSZ): r_B(DK) = 0.099 ± 0.008.

eps png

Constraint on the ratio of amplitudes r_B of the decay B → D^*K: r_B(D^*K) =0.121^+0.018_-0.019.

eps png

Constraint on the ratio of amplitudes r_B of the decay B → DK^*: r_B(DK^*) = 0.118 ± 0.045.

eps png

Constraint on the strong phase between the interfering amplitudes of the decay B → DK from world average D(*)K(*) decays (GLW+ADS) and Dalitz analyses (GGSZ): δ_B(DK) = 110 ± 15 °.

eps png

Constraint on the strong phase between the interfering amplitudes of the decay B → D^*K: δ_B(D^*K) = -55⁺¹⁴_-16°.

eps png

Constraint on the strong phase between the interfering amplitudes of the decay B → DK^*: δ_B(DK^*) = 117⁺³⁰_-42°.

eps png

Constraints on |sin(2β+γ)|:

Constraints on |sin(2β+γ)| from the measurement of time-dependent CP asymmetries in D(*) π(ρ); Winter 11 HFAG average. The extraction of the UT-angle combination relies on SU(3) symmetry for the estimates of the suppressed-to-leading amplitude ratios. We use for r^(*) the values of the branching fractions for D(*) π(ρ) and D_s(*) π(ρ) as averaged by the PDG group (2011 online update), including Babar 2008 and Belle 2010 results. We use our own average for the ratio f_Ds/f_D equal to 1.185 ± 0.005 ± 0.010. According to arXiv:1109.0460 and in lack of unquenched N_f=2+1 computations, we use a conservative value of 1.1 ± 1.1 for the ratios of the decay constants for D_(s)*⁺π^-. We treat the uncertainty on SU(3)-flavour breaking through the method described in Max Baak's thesis (here) with a 10.5% statistic and a 5% systematic uncertainties.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Translation of this result into γ (using sin(2β) as additional input and choosing among the four solutions to the SM one). γ[GLW+ADS+GGSZ+|sin(2β+γ)|] = (68.0 ± 11.0)°.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from |sin(2β+γ)| in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png