Results as of summer 2007 (EPS07/LP07)
Menu:
| The results of the global CKM analysis include: Wolfenstein parameters, UT angles, (combinations of) CKM elements, theory parameters and rare branching fractions. Detailed background information on the methodology and the treatment of experimental and theoretical uncertainties is provided in hep-ph/0406184. |
Numerical Results |
Constraint from the B+→τ+ ν branching fraction:
| α,β,γ convention: | φ1,φ2,φ3 convention: | |
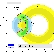
| Constraint in the (ρ-bar,η-bar) plane from the simultaneous use of the the B+→τ+ν branching fraction and Δmd. |
eps gif |

eps gif |
The global CKM fit in the large (ρ-bar,η-bar) plane:
| α,β,γ convention: | φ1,φ2,φ3 convention: | |
| Constraints in the (ρ-bar,η-bar) plane including (a.o.) the most recent α/Φ2- and γ/Φ3-related inputs in the global CKM fit. |

eps gif |

eps gif |
The global CKM fit in the small (ρ-bar,η-bar) plane (zoom):
| α,β,γ convention: | φ1,φ2,φ3 convention: | |
| Zoomed constraints in the (ρ-bar,η-bar) plane including the most recent α/Φ2- and γ/Φ3-related inputs in the global CKM fit. |

eps gif |

eps gif |
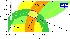
| Zoomed constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit. |
eps gif |

eps gif |
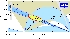
| Constraints in the (ρ-bar,η-bar) plane including only the angle measurements. |
eps gif |

eps gif |
| Constraints from CP conserving quantities (|Vub / Vcb|, Δmd, (Δmd and Δms) and B+ →τ+ ν) in the (ρ-bar,η-bar) plane. |
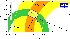
eps gif |

eps gif |
| Constraints from CP violating quantities (sin(2β), α, γ and εk) in the (ρ-bar,η-bar) plane. |
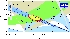
eps gif |

eps gif |
| Constraints from "Tree" quantities in the (ρ-bar,η-bar) plane (γ(DK) and α from the isospin analysis with the help of sin2β (charmonium), which gives another tree only γ measurement (the only assumption is that the ΔI=3/2 b-->d EW penguin amplitude is negligible)). |
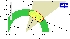
eps gif |

eps gif |
| Constraints from "Loop" quantities in the (ρ-bar,η-bar) plane. |

eps gif |

eps gif |
| Zoomed constraints in the (ρ-bar,η-bar) plane including the angle measurements but sin2β in the global fit. |

eps gif |

eps gif |
Constraints on the angle α/Φ2 from charmless B decays:
|
Constraint on α/Φ2 from B→ππ. Central values (1-CL=1): α(°) = 92.2 ; 128.6 ; 141.5 ; 177.8 1 σ interval: α(°) = ]0.0 ; 7.5] U [82.5 ; 103.1] U [118.0 ; 152.4] U [166.7 ; 180.0[ 2 σ interval: α(°) = ]0.0 ; 14.3] U [75.6 ; 180.0[ |

eps gif |
| The corresponding isospin triangles taking the world averages for the branching fractions and direct CP asymmetries. |
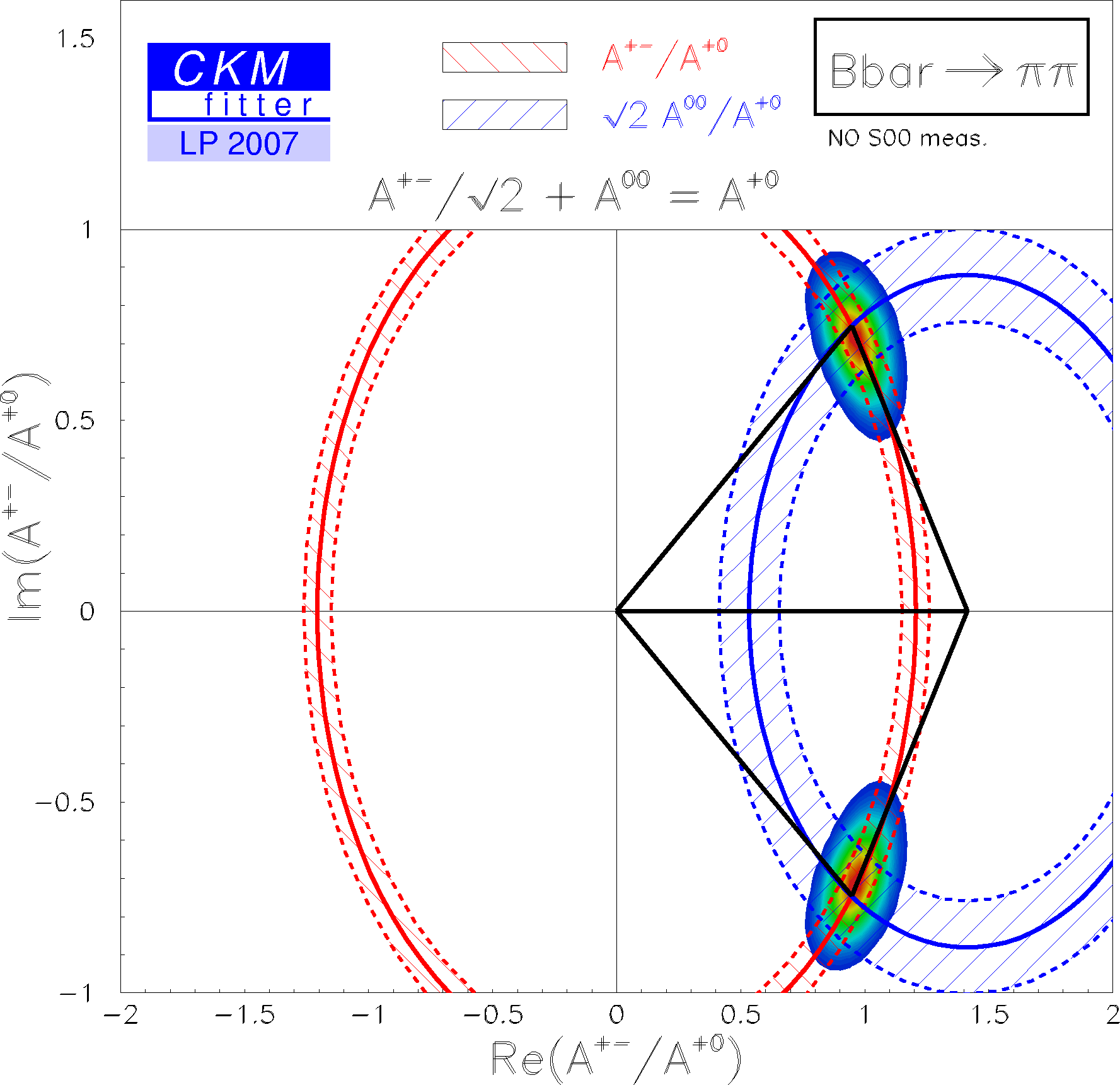
eps gif 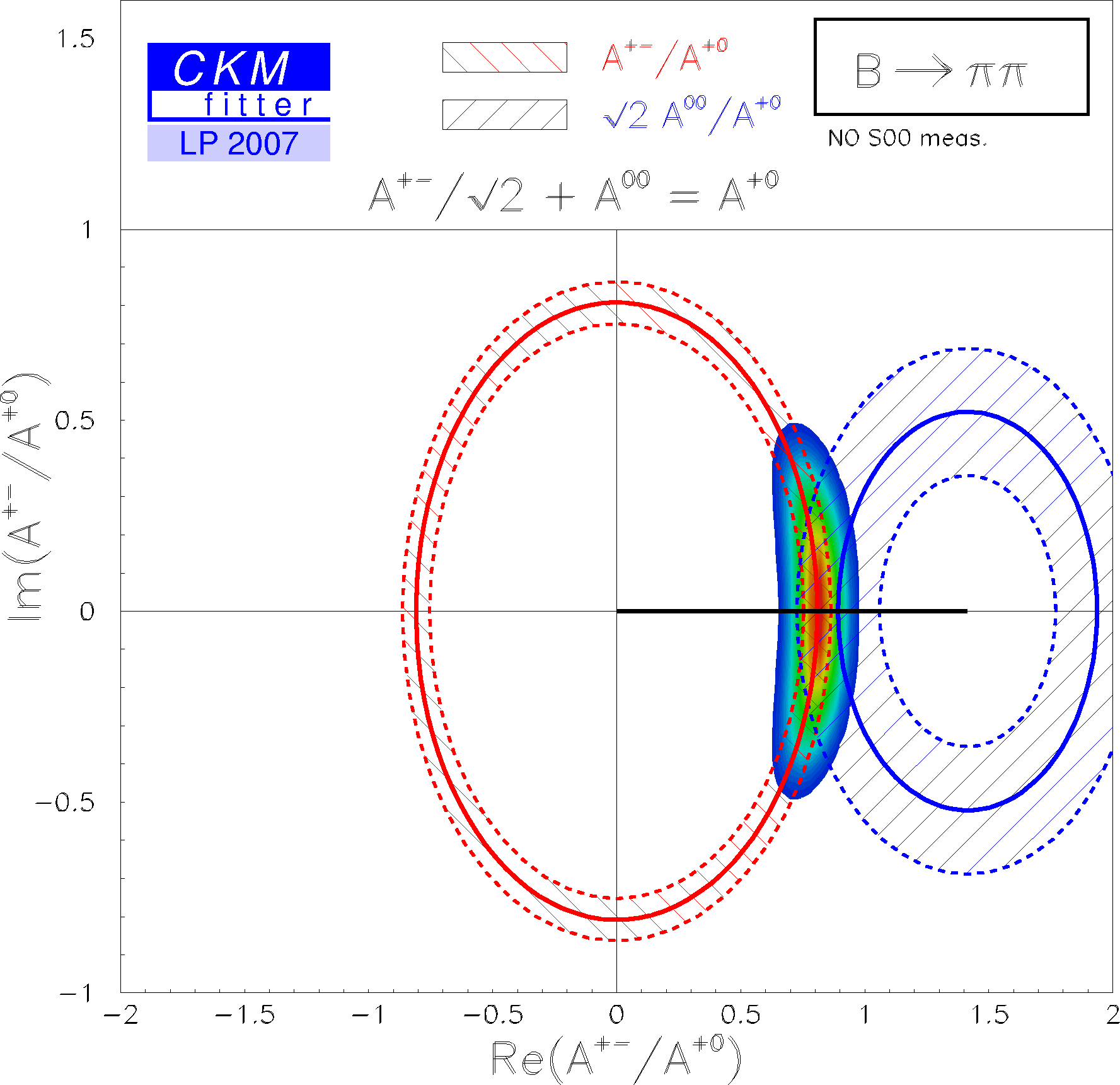
eps gif |
|
Constraint on α/Φ2 from B→ρρ. Central values (1-CL=1): α(°) = 2.9 ; 87.1 1 σ interval: α(°) = ]0.0 ; 14.3] U [ 75.6 ; 97.4] U [172.7 ; 180.0[ 2 σ interval: α(°) = ]0.0 ; 20.1] U [ 69.9 ; 113.4] U [156.5 ; 180.0[ |

eps gif |
| The corresponding isospin triangles taking the world averages for the branching fractions and direct CP asymmetries. |
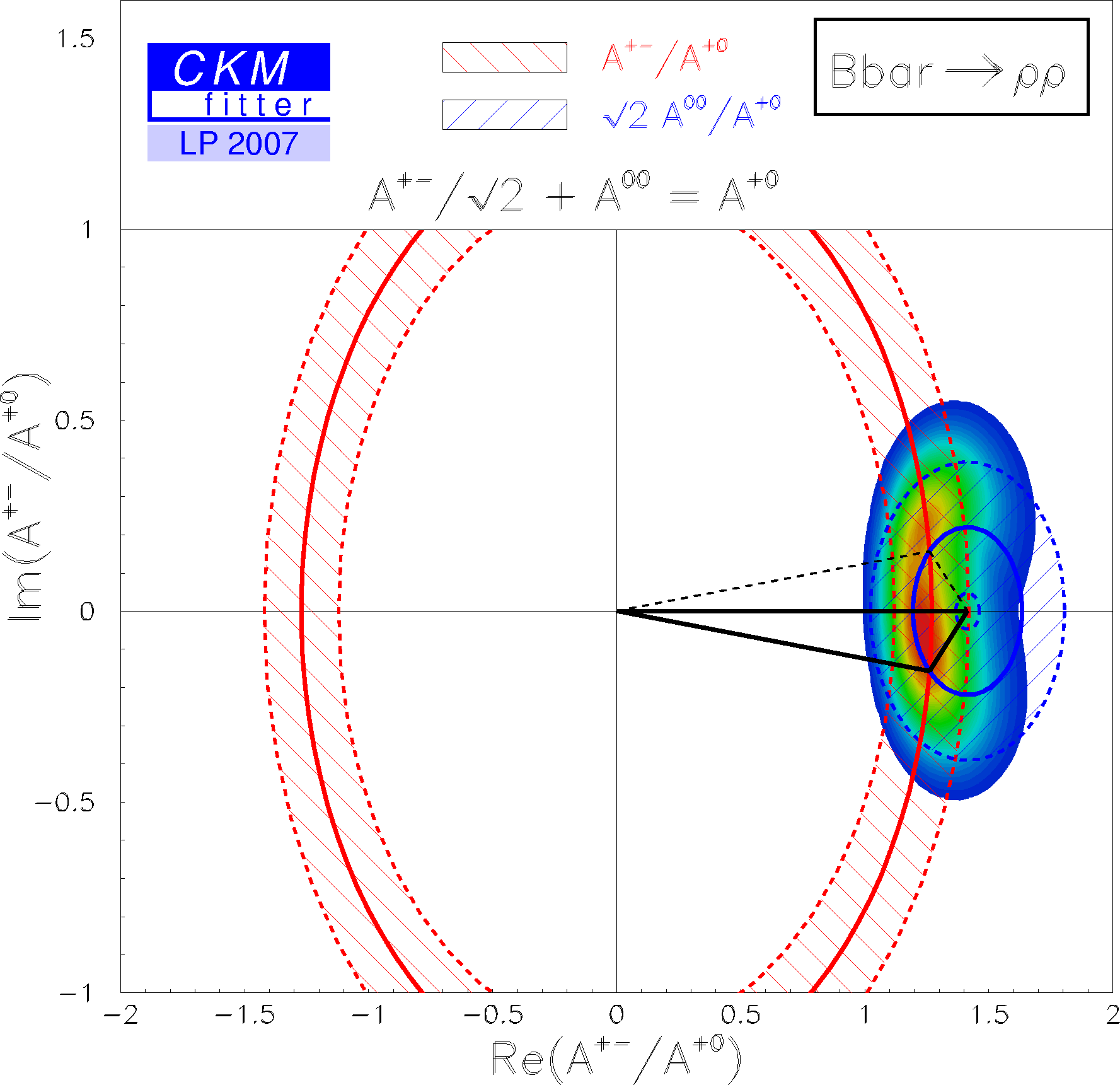
eps gif 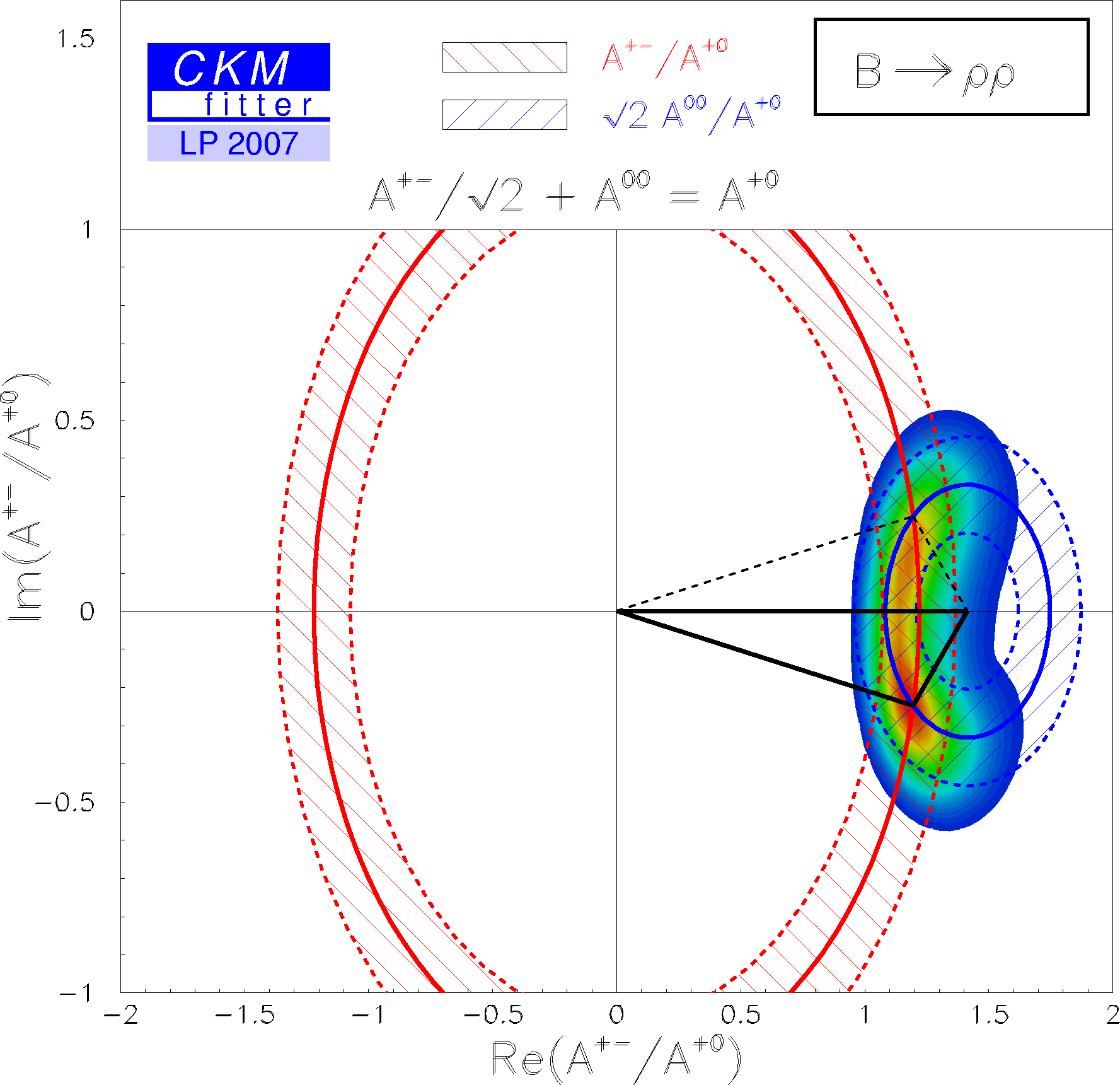
eps gif |
|
Constraint on α/Φ2 from B→ρπ (U and I only).
The global constraint on α from B→ρπ is a combination
of the most recent BABAR and Belle data. This combination is not
just a naive average in α but a combination in the 26
experimentally measured U and I coefficients which are correlated
among each others. The correlation matrices are provided by both
experiments, BABAR and Belle. The combined constraint has a preferred
region around 120 degrees, and two suppressed regions around
30 and 85 degrees. Central value (1-CL=1): α(°) = 119.7 1 σ interval: α(°) = [112.3 ; 130.6] 2 σ interval: α(°) = [ 25.4 ; 37.8] U [105.4 ; 153.6] |

eps gif |
|
Constraints on α/Φ2 from B→ππ (WA), ρπ(WA, Dalitz), ρρ(WA),
compared to the prediction from the CKM fit (not including these measurements). Central value (1-CL=1): α(°) = 87.5 1 σ interval: α(°) = [82.2 ; 93.7] 2 σ interval: α(°) = ]0.0 ; 8.6] U [77.3 ; 118.6] U [163.0 ; 169.7] U [170.3 ; 180.0[ |

eps gif |
Constraints on the angle γ/Φ3
from B decays to charm :
| Constraints on γ/Φ3 from world average D(*)K decays (GLW+ADS) and Dalitz analyses compared to the prediction from the global CKM fit (not including these measurements). &gamma[combined]; = 77 +30 / – 32° |

eps gif |
| Constraints on |sin(2β+γ)| from the measurement of time-dependent CP asymmetries in D(*) π (ρ). Summer 07 HFAG average is used as input. The extraction of the UT angles relies on SU(3) symmetry for the estimates of the suppressed-to-leading amplitude ratios. We use for r(*) the values given in Max Baak's talk presented at CKM06 workshop (here) |
eps gif |
|
Translation of this result into γ (using sin(2β) as additional input and choosing
among the four solutions to the SM one). γ[GLW+ADS+GGSZ+|sin(2β+γ)|] = 80 +19 / – 26° |

eps gif |
| Constraints from |sin(2β+γ)| in the (ρ-bar,η-bar) plane. |

eps gif |