Results as of winter 2007 (MORIOND07/FPCP07)
Please include the following reference when using the CKMfitter plots:
-
CKMfitter Group (J. Charles et al.),
Eur. Phys. J. C41, 1-131 (2005) [hep-ph/0406184],
updated results and plots available at: http://ckmfitter.in2p3.fr
Menu:
The results of the global CKM analysis include: Wolfenstein parameters, UT angles,
(combinations of) CKM elements, theory parameters and rare
branching fractions.
Detailed background information on the methodology and
the treatment of experimental and theoretical uncertainties
is provided in hep-ph/0406184.
|
Numerical Results |
|
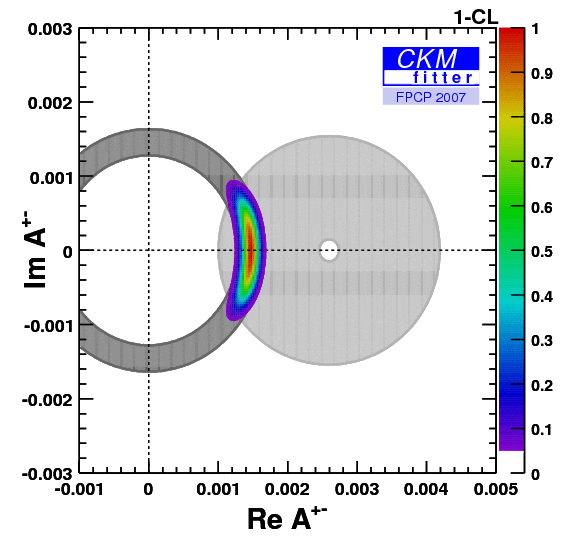
Constraint from the B+→τ+ ν branching fraction:
| α,β,γ convention: | φ1,φ2,φ3 convention: | |
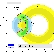
| Constraint in the (ρ-bar,η-bar) plane from the simultaneous use of the the B+→τ+ν branching fraction and Δmd. |
eps gif |

eps gif |
The global CKM fit in the large (ρ-bar,η-bar) plane:
| α,β,γ convention: | φ1,φ2,φ3 convention: | |
| Constraints in the (ρ-bar,η-bar) plane including (a.o.) the most recent α/Φ2- and γ/Φ3-related inputs in the global CKM fit. |

eps gif |

eps gif |
The global CKM fit in the small (ρ-bar,η-bar) plane (zoom):
| α,β,γ convention: | φ1,φ2,φ3 convention: | |
| Zoomed constraints in the (ρ-bar,η-bar) plane including the most recent α/Φ2- and γ/Φ3-related inputs in the global CKM fit. |

eps gif |

eps gif |
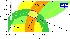
| Zoomed constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit. |
eps gif |

eps gif |
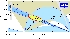
| Constraints in the (ρ-bar,η-bar) plane including only the angle measurements. |
eps gif |

eps gif |
| Constraints from CP conserving quantities (|Vub / Vcb|, Δmd, (Δmd and Δms) and B+ →τ+ ν) in the (ρ-bar,η-bar) plane. |
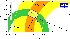
eps gif |

eps gif |
| Constraints from CP violating quantities (sin(2β), α, γ and εk) in the (ρ-bar,η-bar) plane. |
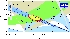
eps gif |

eps gif |
| Constraints from "Tree" quantities in the (ρ-bar,η-bar) plane (γ(DK) and α from the isospin analysis with the help of sin2β (charmonium), which gives another tree only γ measurement (the only assumption is that the ΔI=3/2 b-->d EW penguin amplitude is negligible)). |
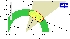
eps gif |

eps gif |
| Constraints from "Loop" quantities in the (ρ-bar,η-bar) plane. |

eps gif |

eps gif |
| Zoomed constraints in the (ρ-bar,η-bar) plane including the angle measurements but sin2β in the global fit. |

eps gif |

eps gif |
Constraints on the angle α/Φ2 from charmless B decays:
| Constraint on α/Φ2 from B→ππ. |

eps gif |
| The corresponding isospin triangles taking the world averages for the branching fractions and direct CP asymmetries. |
eps gif 
eps gif |
| Constraint on α/Φ2 from B→ρρ. |

eps gif |
| The corresponding isospin triangles taking the world averages for the branching fractions and direct CP asymmetries. |
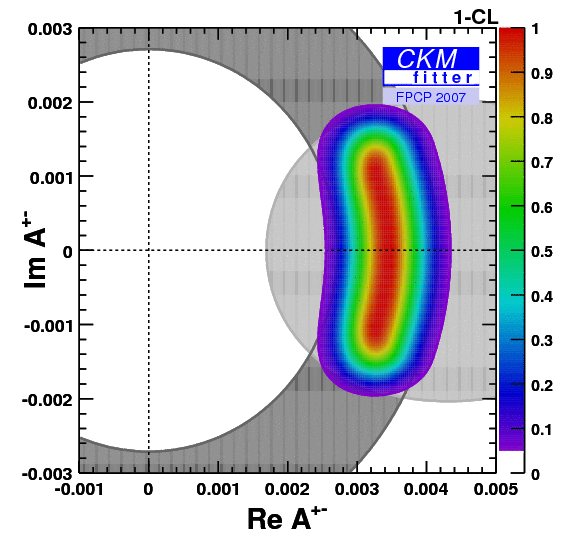
eps gif 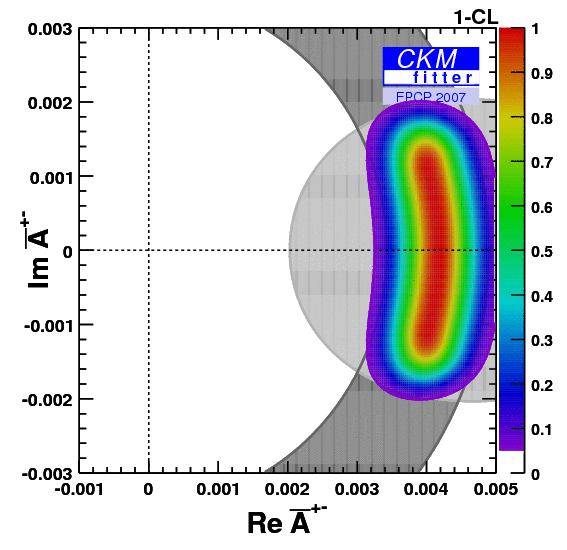
eps gif |
| Constraint on α/Φ2 from B→ρπ (U and I only). The global constraint on α from B→ρπ is a combination of the most recent BABAR and Belle data. This combination is not just a naive average in α but a combination in the 26 experimentally measured U and I coefficients which are correlated among each others. The correlation matrices are provided by both experiments, BABAR and Belle. The combined constraint has a preferred region around 120 degrees, and two suppressed regions around 30 and 85 degrees. |

eps gif |
| Constraints on α/Φ2 from B→ππ (WA), ρπ(WA, Dalitz), ρρ(WA), compared to the prediction from the CKM fit (not including these measurements). The combined constraint on α from B→ρπ does not perfectly fit with the constraints on α from B→ππ and B→ρρ obtained from the isospin analysis. The 120 degree solution does not fit perfectly well with B→ρρ and falls in between two B→ππ solutions. On the other hand, the 85 degree solution is in good agreement with both, B→ππ and B→ρρ. As a consequence, one obtains two preferred regions for α: around 88 degrees and around 115 degrees. |

eps gif |
Constraints on the angle γ/Φ3
from B decays to charm :
| Constraints on γ/Φ3 from world average D(*)K decays (GLW+ADS) and Dalitz analyses compared to the prediction from the global CKM fit (not including these measurements). |

eps gif |
New physics in B0- B0bar Mixing
New physics (NP) in B0q-B0qbar Mixing
(q = d, s) can be described model-independently by introducing two new parameters
measuring the relative strength (rq2) and the relative phase
(2*Θq) between the B0- B0bar mixing
matrix element containing contributions from the Standard Model (SM) as well as
from NP contributions (full) compared to SM contributions only:
|
||
|
Assuming that NP is short-distance dominated it only contributes to M12 whereas Γ12 is unaffected. As a consequence:
|
||
|
An alternative parametrisation is given by:
|
||
|
Constraints from |Vud|, |Vus|, |Vcb|, |Vub|, Δmd=ΔmdSM * rd2 and sin(2β+2Θd) in the (rd2,2*Θd) plane. The inputs have been taken from CKM2006. The corresponding constraint in the (ρ-bar,η-bar) is just given by the circle obtained from the inputs |Vud|, |Vus|, |Vcb|, |Vub| alone since there are four free parameters in the fit (ρ-bar,η-bar,rd2,2*Θd) but only three constraints (|Vub|, sin(2β+2Θd), Δmd=ΔmdSM * rd2) depend on those. As a consequence, the allowed region in the (rd2,2*Θd) plane is rather large. |
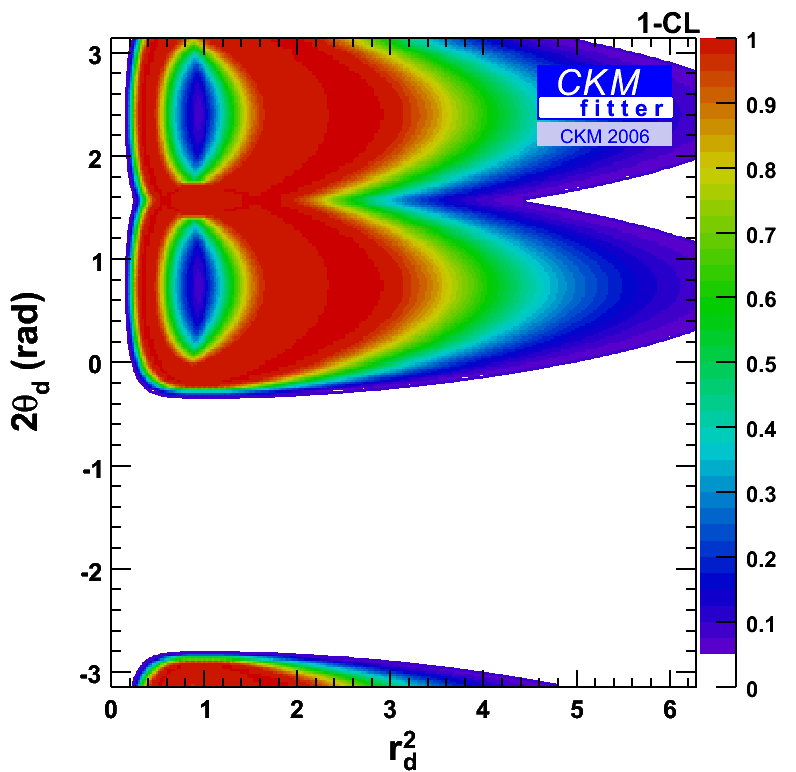 gif 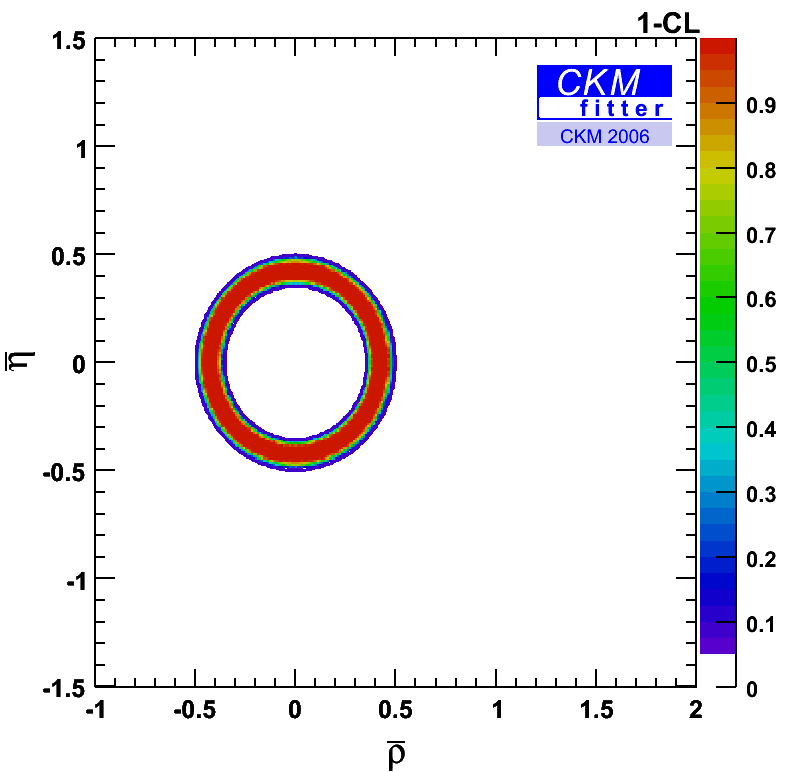 gif |
|
|
When using in addition the following inputs: cos(2β) > 0 (suggested by data), α (ππ, 3π, ρρ), and γ, the allowed regions are substantially reduced in the (rd2,2*Θd) plane. |
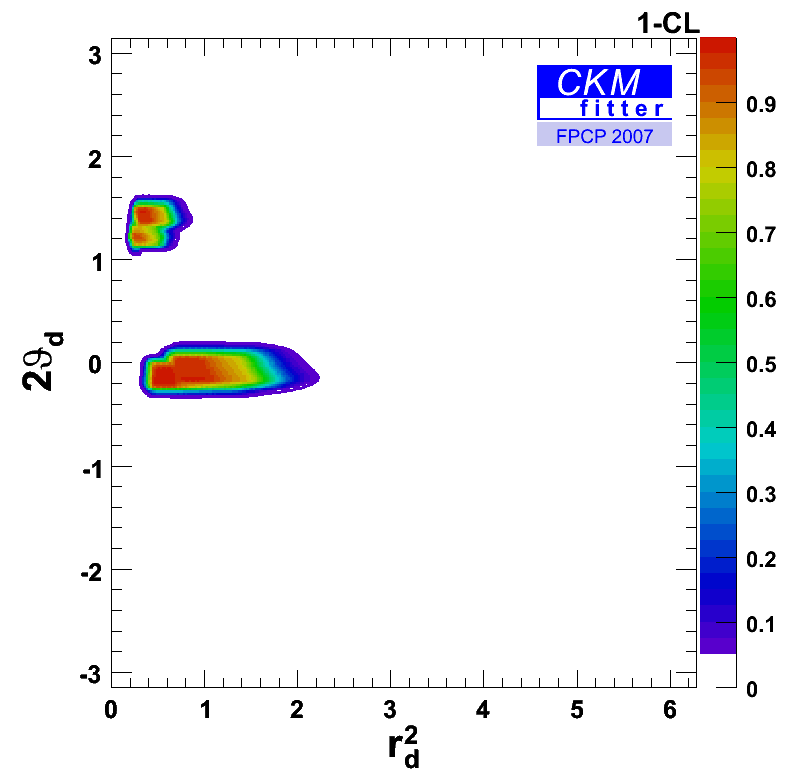 eps gif |
|
|
There are two allowed regions left. One region is close to the SM expectation (rd2=1,2*Θd=0) and another one clearly differing from the SM solution. Both regions show a doublepeak substructure. This structure is caused by the current α input which has two preferred regions in alpha. |
||
|
The non-SM-like region can be suppressed by ASLd, the dilepton CP asymmetry, in the Bd sector. The inclusive dilepton asymmetry ASL measured by D0 which is a mixture of ASLd and ASLs can be used as well. When combining both inputs one has to allow also for NP in the Bs sector. Hence, a combined analysis for the Bd and Bs sector is performed. |
||
|
The additional inputs used are then ASLd, ASL, ASLs measured by D0 (which has currently a quite large uncertainty), Δms=ΔmsSM*rs2, and ΔΓsCP' = ΔΓsSM*cos2(2*Θs) (measured by D0). The result in the (rd2,2*Θd) plane shows that the non-SM solution is significantly suppressed. Also the relative Confidence Level between the two peaks inside the SM-like region changes as the dilepton asymmetries prefer a negative sign. |
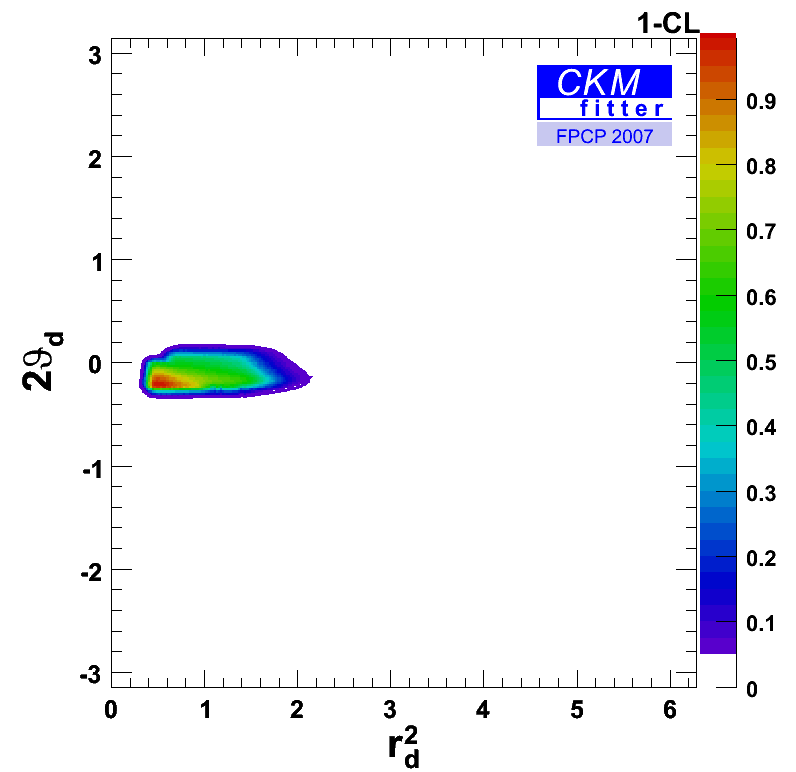 eps gif |
|
|
This is better illustrated in the (ρ-bar,η-bar) plane: |
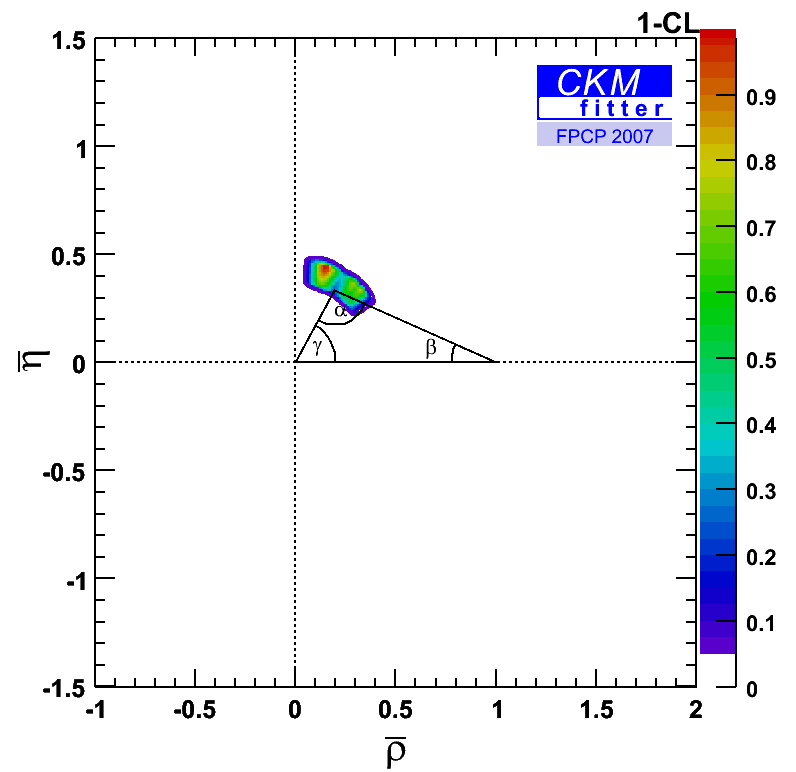 eps gif |
|
|
The corresponding plot in the (hd,2*σd) plane. |
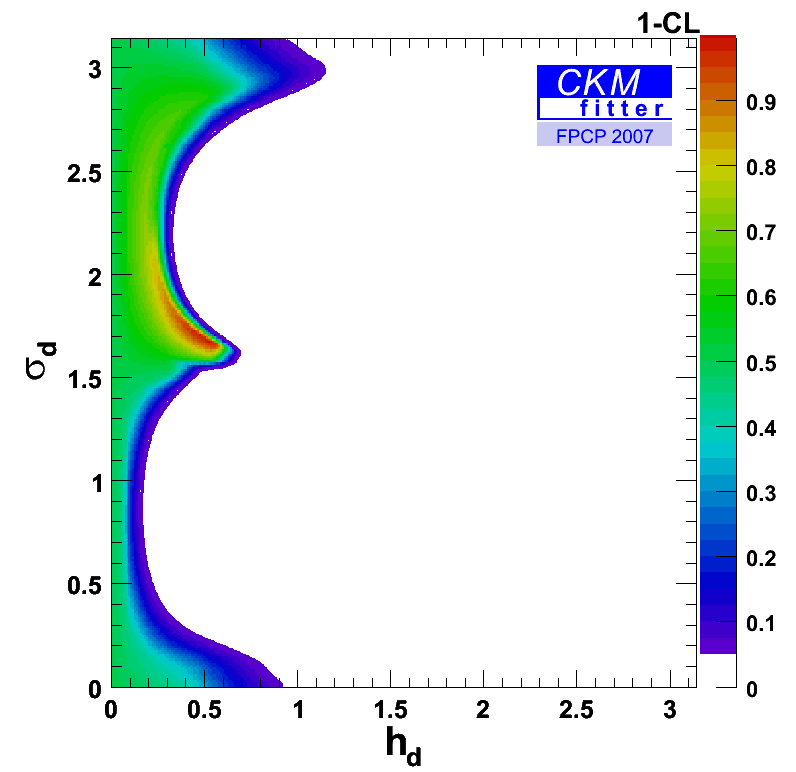 eps gif |
|
|
The constraint in the (rs2,2*Θs) plane shows a strong constraint on rs2 due to the Δms measurement from CDF. Since the central value of ΔΓsCP' is larger than the ΔΓsSM prediction regions around 2*Θs=+-π/2 are currently disfavoured. |
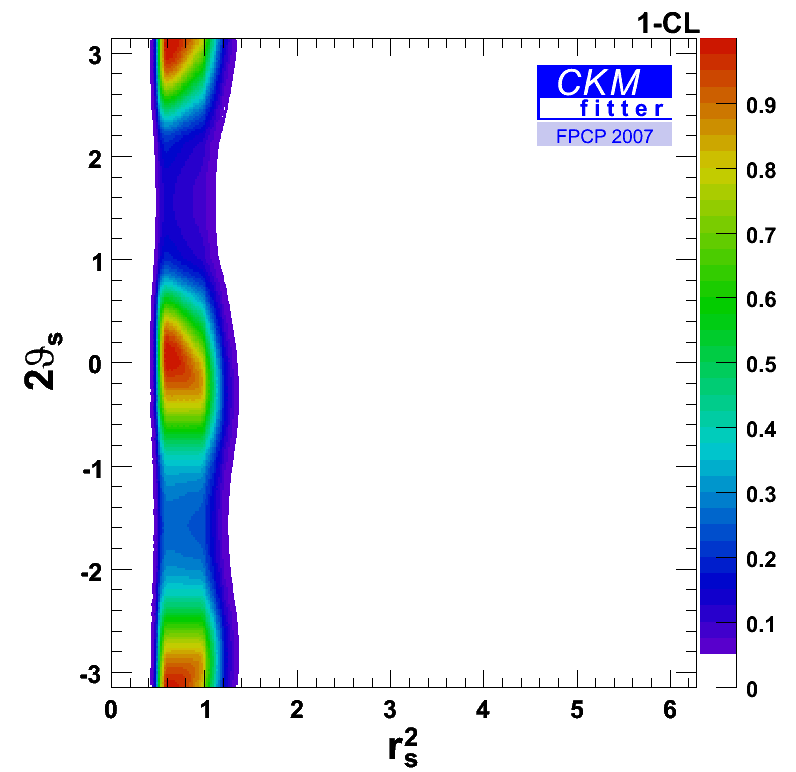 eps gif |
|
|
The corresponding constraint in the (hs,2*σs) plane. |
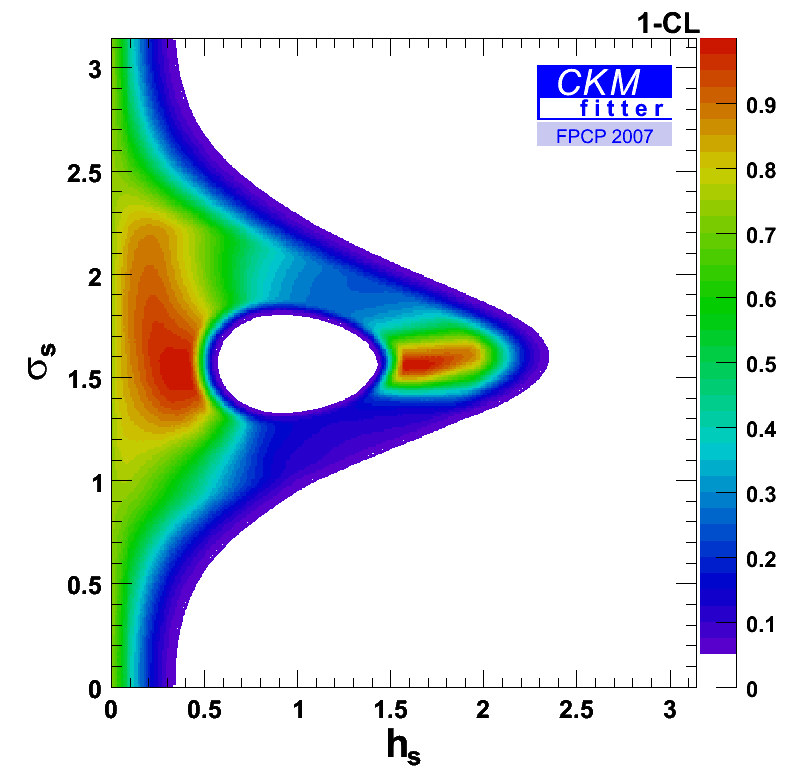 eps gif |
|