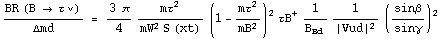CKMfitter

Preliminary results as of Summer 2012
(ICHEP 12 conference)

Menu:

The global CKM fit: Inputs and Numerical results

The global CKM fit in the large (ρ-bar,η-bar) plane

Constraint from BR(B⁺→τ⁺ ν)

New physics in neutral-meson mixing

Branching ratio of B_s→μ⁺ μ^-

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom)

The global CKM fit in the large (ρ_s-bar,η_s-bar) plane

The global CKM fit in the (|V_ud|,|V_us|) plane

The global CKM fit in the (|V_cd|,|V_cs|) plane

Constraints on the angle α/ϕ₂ from charmless B decays

Constraints on the angle γ/ϕ₃ from B decays to charm

Constraints on |sin(2β+γ)|

Numerical results:

The results of the global CKM analysis include:

Wolfenstein parameters,
UT angles and sides,
UT_sangle and apex,
CKM elements,
theory parameters,
rare branching fractions (B->lν, B->ll).

Numerical Results

The global CKM fit in the large (ρ-bar,η-bar) plane:

Constraints in the (ρ-bar,η-bar) plane. The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane. The |V_ub| constraint has been split in the two contributions: |V_ub| from inclusive and exclusive semileptonic decays (plain dark green) and |V_ub| from B⁺→τ⁺ ν (hashed green). The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

One notices that the ring coming from the combined constraint from Δ m_d and Δ m_s is cut for values of ρ close to 2. This can be understood by the fact that the two constraints provide ranges respectively on

|V_td|²=A² λ⁶ [(1-ρ)²+η²+O(λ⁴)]

|V_ts|²=A² λ⁴ [1-λ²(1-2 ρ)+O(λ⁴)]

The 68% and 95% CL constraints on ρ from Δ m_s are indicated in the two shades of red, together with the (circular) constraint from Δ m_d and the mended ring once the two constraints are combined.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraint from the B⁺→τ⁺ ν branching ratio:

A new value of BR(B→τν) from Belle has led to a decrease of the world average. The discrepancy in the CKM global fit between the world averages for sin2β and BR(B→τν) has thus been eased significantly.

There is a specific correlation between the two quantities in the global fit, which is best viewed in the (sin2β,BR(B→τν)) plane, regarding the prediction from the global fit without using these measurements. The cross corresponds to the experimental value with 1 sigma errors.

eps png

The shape of the correlation can be understood by considering the ratio BR(B→τν)/Δm_d, where the decay constant f_{B_d} cancels, leaving limited theoretical uncertainties (the ratio depends only on the bag parameter B_{B_d}). Thus from the observables BR(B→τν) and Δm_d one gets an interesting constraint in the (ρbar,ηbar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

To have a closer look, one can write the full formula for the ratio

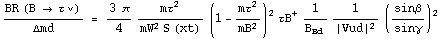
where one explicitly sees that the correlation between BR(B→τν) and the angle β is controlled by the values of B_{B_d}, and the angles α and γ. This can be checked explicitly by comparing the above analytical formula with the colored region in the (sin2β,BR(B→τν)) plane.

To quantify the discrepancy one can compare the indirect fit prediction for BR(B→τν) with the measurement. The deviation here is 1.6 sigmas.

eps png

A simpler test is the comparison of the prediction of B_{B_d} from the above analytical formula B_{B_d} = 0.80^+0.23_-0.16 (having only BR(B→τν), Δm_d, α, β, γ and |V_ud| as inputs, that is an almost completely theory-free determination of B_{B_d}), with the current lattice determination B_{B_d} = 1.29 ^+0.08_-0.08. For this test the deviation is 1.4 sigmas.

eps png

New physics in neutral-meson Mixing:

Individual constraints correspond to 68% CL (see: arXiv:1008.1593 [hep-ph] and arXiv:1203.0238. [hep-ph] for a detailed explanation of the hypotheses). These plots have been obtained with the following updates:

(φ_s,ΔΓ_s) likelihood provided by HFAG averaging D0, CDF and LHCb results for B_s→J/_Ψ φ,
the new HFAG average for a_SL^d=0.0038±0.0036
the average of the LHCb [LHCb-CONF-2012-022] and D0 [0904.3907] results for a_SL^s=-0.0022±0.0052.

In scenario I we have introduced NP in M₁₂^q = M₁₂^SM,qΔ_q independently for B_d, B_s and K, corresponding to NP with arbitrary flavour structure.

Constraints on New Physics in the (ReΔ_d,ImΔ_d) plane. A 1.6 σ deviation is obtained for the 2-dimensional SM hypothesis Δ_d = 1 (Re(Δ_d)=1, Im(Δ_d)=0).

eps png

Constraints on New Physics in the (ReΔ_s,ImΔ_s) plane. A 0.2 σ deviation is obtained for the 2-dimensional SM hypothesis Δ_s = 1 (Re(Δ_s)=1, Im(Δ_s)=0).

The pulls for the relevant observables are 0.1 σ for B->τν, 2.8 σ for φ_s^{J/Ψ Φ} and 3.3 σ for A_SL, illustrating the difficulty to accomodate the last two results in this scenario.

eps png

Indirect constraint on the asymmetry A_SL=(-7.5^+5.0_-6.3)x10^-4 or (44.7^+9.7_-7.1)x10^-4, compared with the direct measurements of CDF and D0. A second solution is now allowed due to the update of the input for a_SL^d.

eps png

Indirect constraint on the CP phase φ_s^{J/Ψ Φ}=-61.8^+10.5_-7.1 degrees, compared with the direct measurements of CDF, D0 and LHCb.

eps png

Branching ratio of B_s→μ⁺ μ^-

Prediction for Br(B_s→μ⁺ μ^-)=(3.63^+0.21_-0.34)x10^-9. The blue (respectively red) curve represents the prediction removing the input from Δ m_s (respectively f_{B_s}). The red curve is actually identical to the green one, indicating that the prediction is dominated by the indirect determination of f_{B_s} through the global fit (more specifically Δm_s), and not by its direct input.

eps png

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom):

Zoomed constraints in the (ρ-bar,η-bar) plane.The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Zoomed constraints in the (ρ-bar,η-bar) plane. The |V_ub| constraint has been split in the two contributions: |V_ub| from inclusive and exclusive semileptonic decays (plain dark green) and |V_ub| from B⁺→τ⁺ ν (hashed green). The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Zoomed constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane including only the angle measurements.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from CP conserving quantities (|V_ub / V_cb|, Δm_d, (Δm_d and Δm_s) and B⁺ →τ⁺ ν) in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from CP violating quantities (sin(2β), α, γ and ε_k) in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from "Tree" quantities in the (ρ-bar,η-bar) plane (γ(DK) and α from the isospin analysis with the help of sin2β (charmonium), which gives another tree only γ measurement (the only assumption is that the ΔI=3/2 b-->d EW penguin amplitude is negligible)).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from "Loop" quantities in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane, not including the braching ratio of B⁺ → τ⁺ν in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane not including the measurement of sin2β in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

The global CKM fit in the (|V_ud|,|V_us|) plane:

Constraints in the (|V_ud|,|V_us|) plane. The indirect constraints (coming from b transitions) are related to |V_ud| and |V_us| through unitarity.

eps png

The global CKM fit in the (|V_cd|,|V_cs|) plane:

Constraints in the (\|V_cd\|,\|V_cs\|) plane. The indirect constraints (coming from b and s transitions) are related to \|V_cd\| and \|V_cs\| through unitarity. The direct constraints combine leptonic and semileptonic D and D_s decays as well as information from neutrino-nucleon scattering and W → cs decays. The following plots correspond to different subsets of these constraints.	eps png
Constraints in the (\|V_cd\|,\|V_cs\|) plane where direct constraints involve only leptonic D and D_s decays with our inputs for lattice averages f_Ds/f_D=1.185 ± 0.005 ± 0.010 and f_Ds=249.2 ± 1.2 ± 4.5 MeV.	eps png
Constraints in the (\|V_cd\|,\|V_cs\|) plane where direct constraints involve only semileptonic D and D_s decays with our inputs for lattice averages F_{D → π}(0)=0.666 ± 0.017 ± 0.048 and F_{D → K}(0)=0.747 ± 0.010 ± 0.034.	eps png
Constraints in the (\|V_cd\|,\|V_cs\|) plane where direct constraints involve only information from neutrino-nucleon scattering and W→ cs decays (no lattice input).	eps png

Constraints on the angle α/ϕ₂ from charmless B decays:

No update

See Winter 12 results (here).

Constraints on the angle γ/ϕ₃ from B decays to charm :

No update

See Winter 12 results (here).

Constraints on |sin(2β+γ)|:

No update

See Winter 12 results (here).