CKMfitter

Preliminary results as of Spring 2013
(FPCP 2013 conference)

Menu:

The global CKM fit: Inputs and Numerical results

The global CKM fit in the large (ρ-bar,η-bar) plane

Constraints on the angle α/ϕ₂ from charmless B decays

Constraints on the angle γ/ϕ₃ from B decays to charm

New physics in neutral-meson mixing

Branching ratio of B_s→μ⁺ μ^-

The global CKM fit in the (|V_ud|,|V_us|) plane

The global CKM fit in the (|V_cd|,|V_cs|) plane

Constraint from BR(B⁺→τ⁺ ν)

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom)

Inputs and numerical results:

The results of the global CKM analysis include:

Wolfenstein parameters,
UT angles and sides,
UT_sangle and apex,
CKM elements,
input parameters,
rare decay branching fractions.

Numerical Results

The global CKM fit in the large (ρ-bar,η-bar) plane:

Constraints in the (ρ-bar,η-bar) plane. The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane. The |V_ub| constraint has been splitted in the two contributions: |Vub| from inclusive and exclusive semileptonic decays (plain dark green) and |Vub| from B⁺→τ⁺ ν (hashed green). The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on the angle α/ϕ₂ from charmless B decays:

Constraints on α/ϕ₂ from B→ρπ (BABAR, Belle and WA), with

α[WA,ρπ]=(54.1^+7.7_-10.3)° or (141.8^+4.7_-5.4)°
compared to the prediction from the global CKM fit (not including the α-related measurements)

α[fit]=(94.9^+4.8_-6.8)°

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on α/ϕ₂ from the combination of B→ππ, ρπ, and ρρ for BABAR, Belle and WA, with

α[WA,all]=(85.4^+4.0_-3.8)°
compared to the prediction from the global CKM fit (not including the α-related measurements).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on α/ϕ₂ from B→ππ, ρπ and ρρ (WA) compared to the prediction from the global CKM fit (not including the α-related measurements).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints on the angle γ/ϕ₃ from B decays to charm:

The references of the observables from charged B → D^(*)K^(*) decays (GLW+ADS) and Dalitz analyses (GGSZ) from BaBar, Belle, LHCb are included in the summary of inputs and results file

We also use the inputs from charm (combining observables from charm mixing, CPV and ψ(3770) results):

δ_D(Kπ) = (202.6^+7.6_-8.9)°
δ_D(K3π) versus R_K3π

eps png

Constraints on γ combining results from D^(*)K^(*) decays (GLW+ADS) and Dalitz analyses (GGSZ) from BaBar, Belle, LHCb and world average :
γ[combined] = (68.0^+8.0_-8.5)°,
compared to the prediction from the global CKM fit (not including these measurements): γ[fit] = (69.7^+1.3_-2.8)°

eps png

Constraints on γ from world average D^(*)K^(*) decays (GLW+ADS) and Dalitz analyses (GGSZ) (methods shown separately):

γ[BaBar] = (69 ± 17)°
γ[Belle] = (68 ± 14)°
γ[LHCb] = (69⁺¹¹_-13)°
γ[combined] = (68.0^+8.0_-8.5)°

eps png	eps png
eps png	eps png

Constraint on the ratio of interfering amplitudes r_B of the decay B → DK from world average D^(*)K^(*) decays (GLW+ADS) and Dalitz analyses (GGSZ):

r_B(DK) = 0.0956^+0.0062_-0.0064
r_B(D^*K) =0.121^+0.018_-0.019
r_B(DK^*) = 0.140^+0.044_-0.047

eps png

Constraint on the strong phase between the interfering amplitudes of the decay B → DK from world average D^(*)K^(*) decays (GLW+ADS) and Dalitz analyses (GGSZ):

δ_B(DK)=(114.8^+9.0_-9.7)°
δ_B(D^*K)=(-55⁺¹³_-14)°
δ_B(DK^*)=(110⁺³¹_-42)°

eps png

Illustration of the correlation between the determination of γ and the ratio of interfering amplitudes r_B (the strong phase difference δ_B) of the decay B → DK from world average D^(*)K^(*) decays (GLW+ADS) and Dalitz analyses (GGSZ).

r_B versus γ	δ_B versus γ
eps png	eps png

Same using only Babar inputs.

eps png

Same using only Belle inputs.

eps png

Same using only LHCb inputs.

eps png

Illustrations of the correlation between the determination of γ determined with the GLW+ADS observables and the strong phase difference δ_D for BaBar, Belle, LHCb and all experiments combined.

eps png	eps png
eps png	eps png

Comparison of the strong phase δ_D(Kπ) obtained from charm inputs (green dotted), from GLW+ADS observables (blue) and from GLW+ADS+GGSZ observables (red)

eps png

New physics in neutral-meson Mixing:

Individual constraints correspond to 68% CL (see: arXiv:1008.1593 [hep-ph] and arXiv:1203.0238 [hep-ph] for a detailed explanation of the hypotheses).

Numerical inputs, results and confidence intervals are given in the detailed discussion of inputs and results.

In scenario I we have introduced NP in M₁₂^q = M₁₂^SM,qΔ_q independently for B_d, B_s and K, corresponding to NP with arbitrary flavour structure. Constraints on New Physics in the (ReΔ_d,ImΔ_d) plane. A 1.5 σ deviation is obtained for the 2-dimensional SM hypothesis Δ_d = 1 (Re(Δ_d)=1, Im(Δ_d)=0).	eps png
Constraints on New Physics in the (ReΔ_s,ImΔ_s) plane. A 0.0 σ deviation is obtained for the 2-dimensional SM hypothesis Δ_s = 1 (Re(Δ_s)=1, Im(Δ_s)=0). The pulls for the relevant observables are 0.2 σ for B->τν, 2.9 σ for φ_s^{J/Ψ Φ} and 3.4 σ for A_SL, illustrating the difficulty to accomodate the last two results in this scenario.	eps png

Branching ratio of B_s→μ⁺ μ^-

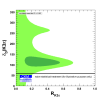
Prediction for Br(B_s→μ⁺ μ^-)=(3.63^+0.21_-0.34)x10^-9. The blue (respectively red) curve represents the prediction removing the input from Δ m_s (respectively f_{B_s}). The red curve is actually identical to the green one, indicating that the prediction is dominated by the indirect determination of f_{B_s} through the global fit (more specifically Δm_s), and not by its direct input.

eps png

The global CKM fit in the (|V_ud|,|V_us|) plane:

Constraints in the (\|V_ud\|,\|V_us\|) plane. The indirect constraints (coming from b transitions) are related to \|V_ud\| and \|V_us\| through unitarity. The red hashed region of the global combination corresponds to 68% CL.	eps png
The accuracy recently reached by kaon leptonic decays K→eν and K→μν requires the inclusion of the full set of universal radiative corrections described in Marciano-Sirlin 1993. The agreement is then very good between the measurements and the prediction of the global fit without these observables.	eps png

The global CKM fit in the (|V_cd|,|V_cs|) plane:

Constraints in the (\|V_cd\|,\|V_cs\|) plane. The indirect constraints (combing from b and s transitions) are related to \|V_cd\| and \|V_cs\| through unitarity. The direct constraints combine leptonic and semileptonic D and D_s decays as well as information from neutrino-nuclaon scattering and W → cs decays. The red hashed region of the global combination corresponds to 68% CL.	eps png
Constraints in the (\|V_cd\|,\|V_cs\|) plane where direct constraints involve only leptonic D and D_s decays with our inputs for lattice averages.	eps png
Constraints in the (\|V_cd\|,\|V_cs\|) plane where direct constraints involve only semileptonic D and D_s decays with our inputs for lattice averages.	eps png
Constraints in the (\|V_cd\|,\|V_cs\|) plane where direct constraints involve only information from neutrino-nucleaon scattering and W→ cs decays (no lattice input).	eps png

Constraint from the B⁺→τ⁺ ν branching ratio:

The recent update of BR(B→τν) from Belle has led to a decrease of the world average. The discrepancy in the CKM global fit between the world averages for sin2β and BR(B→τν) has thus been eased significantly.
There is a specific correlation between the two quantities in the global fit which is best viewed in the (sin2β,BR(B→τν)) plane, regarding the prediction from the global fit without using these measurements. The cross corresponds to the experimental value with 1 sigma errors.	eps png
The constraint can also be seen from the point of view of lattice inputs, with the predictions on the decay constant f_{B_d} and f_{B_d} Sqrt[B_{B_d}]	eps png

The global CKM fit in the small (ρ-bar,η-bar) plane (zoom):

Zoomed constraints in the (ρ-bar,η-bar) plane.The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Zoomed constraints in the (ρ-bar,η-bar) plane. The |V_ub| constraint has been splitted in the two contributions: |V_ub| from inclusive and exclusive semileptonic decays (plain dark green) and |V_ub| from B⁺→τ⁺ ν (hashed green). The red hashed region of the global combination corresponds to 68% CL.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Zoomed constraints in the (ρ-bar,η-bar) plane not including the angle measurements in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane including only the angle measurements.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from CP conserving quantities (|V_ub / V_cb|, Δm_d, (Δm_d and Δm_s) and B⁺ →τ⁺ ν) in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from CP violating quantities (sin(2β), α, γ and ε_k) in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from "Tree" quantities in the (ρ-bar,η-bar) plane (γ(DK) and α from the isospin analysis with the help of sin2β (charmonium), which gives another tree only γ measurement (the only assumption is that the ΔI=3/2 b-->d EW penguin amplitude is negligible)).

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints from "Loop" quantities in the (ρ-bar,η-bar) plane.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane, not including the braching ratio of B⁺ → τ⁺ν in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png

Constraints in the (ρ-bar,η-bar) plane not including the measurement of sin2β in the global fit.

α, β, γ convention	ϕ₁, ϕ₂, ϕ₃ convention
eps png	eps png